题目内容
(Ⅰ)求极坐标方程ρsin2θ-2•cosθ=0表示的曲线的焦点坐标;
(Ⅱ)设直线l:
(t为参数)与题(Ⅰ)中的曲线交于A、B两点,若P(2,3),求|PA|•|PB|的值.
(Ⅱ)设直线l:
|
分析:(I)求得曲线的直角坐标方程为 x2=4y,求得它的焦点坐标为(0,1),再化为极坐标即可.
(II)把直线方程代入曲线的方程化简可得
t2+
t+5=0,利用根与系数的关系,以及|PA|=|t1|,|PB|=|t2|求出|PA|•|PB|.
(II)把直线方程代入曲线的方程化简可得
| 16 |
| 25 |
| 18 |
| 5 |
解答:解:(1)解(1)由ρ•ρsin2θ-ρ•2•cosθ=0
得y2=2x------------(4分)
焦点(
,0)------------(6分)
(2)设A,B两点对应的参数分别为t1,t2,
将
代入y2=2x------------(9分)
得
t2+
t+5=0------------(11分)
∴t1t2=
即|PA|•|PB|=|t1t2|=
------------(14分)
得y2=2x------------(4分)
焦点(
| 1 |
| 2 |
(2)设A,B两点对应的参数分别为t1,t2,
将
|
得
| 16 |
| 25 |
| 18 |
| 5 |
∴t1t2=
| 125 |
| 16 |
即|PA|•|PB|=|t1t2|=
| 125 |
| 16 |
点评:本题考查点的极坐标与直角坐标的互化,抛物线的标准方程和简单性质的应用,考查求直线的参数方程的方法,把极坐标方程化为普通方程的方法,以及直线方程中参数的意义.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
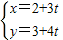 (t为参数)与题(Ⅰ)中的曲线交于A、B两点,若P(2,3),求|PA|•|PB|的值.
(t为参数)与题(Ⅰ)中的曲线交于A、B两点,若P(2,3),求|PA|•|PB|的值.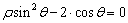 表示的曲线的焦点坐标;
表示的曲线的焦点坐标; :
: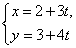 (
(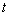 为参数)与题(Ⅰ)中的曲线交于A、B两点,若P(2,3),
为参数)与题(Ⅰ)中的曲线交于A、B两点,若P(2,3),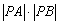 的值.
的值.