Question

（本小题满分12分）已知数列{a_n}，a₁＝1，a_n＝λa_n－1＋λ－2（n≥2）．

（1）当λ为何值时，数列{a_n}可以构成公差不为零的等差数列，并求其通项公式；

（2）若λ＝3，求数列{a_n}的通项公式a_n．

 

 

Answer 1

【答案】

解　（1）a₂＝λa₁＋λ－2＝2λ－2，

a₃＝λa₂＋λ－2＝2λ²－2λ＋λ－2＝2λ²－λ－2，

∵a₁＋a₃＝2a₂，∴1＋2λ²－λ－2＝2（2λ－2），

得2λ²－5λ＋3＝0，解得λ＝1或λ＝．

当λ＝时，a₂＝2×－2＝1，a₁＝a₂，故λ＝不合题意舍去；

当λ＝1时，代入a_n＝λa_n－1＋λ－2可得a_n－a_n－1＝－1，

∴数列{a_n}构成首项为a₁＝1，d＝－1的等差数列，

∴a_n＝2－n．

（2）当λ＝3时，a_n＝3a_n－1＋1，

即a_n＋＝3（a_n－1＋），令b_n =a_n＋

即b_n＝3b_n－1，

∴数列{b_n}构成首项为b₁＝，公比为3的等比数列，

∴b_n＝×3^n－1＝，

∴a_n=-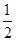

 

【解析】略