题目内容
(本小题满分10分)已知数列 的前
的前 项和
项和 ,
, 求 数列
求 数列 的通项公式及数列
的通项公式及数列 的前
的前 项和
项和 。
。
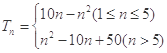
解析

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
设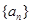 是公比为
是公比为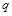 的等比数列,令
的等比数列,令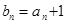 ,
,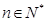 ,若数列
,若数列 的连续四项在集合
的连续四项在集合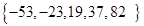 中,则
中,则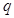 等于( )
等于( )
A.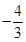 | B.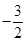 | C.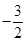 或 或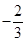 | D.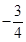 或 或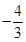 |
题目内容
(本小题满分10分)已知数列 的前
的前 项和
项和 ,
, 求 数列
求 数列 的通项公式及数列
的通项公式及数列 的前
的前 项和
项和 。
。
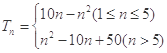
解析

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案设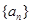 是公比为
是公比为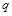 的等比数列,令
的等比数列,令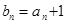 ,
,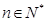 ,若数列
,若数列 的连续四项在集合
的连续四项在集合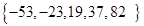 中,则
中,则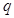 等于( )
等于( )
A.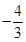 | B.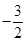 | C.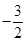 或 或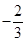 | D.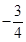 或 或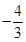 |