题目内容
【题目】已知![]() 是椭圆
是椭圆![]() :
:![]() 的左焦点,
的左焦点,![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个相异动点,若
上的两个相异动点,若![]() 中点的横坐标为1,则
中点的横坐标为1,则![]() 到直线
到直线![]() 距离的最小值为______.
距离的最小值为______.
【答案】![]()
【解析】
分直线![]() 的斜率存在和不存在两种情况讨论,由于同一点对称性设斜率大于0,与椭圆联立求出两根之和,再由
的斜率存在和不存在两种情况讨论,由于同一点对称性设斜率大于0,与椭圆联立求出两根之和,再由![]() 的中点的横坐标求出参数之间的关系,由点到直线的距离公式求出
的中点的横坐标求出参数之间的关系,由点到直线的距离公式求出![]() 到直线
到直线![]() 距离.令参数部分为函数,求导,由函数的单调性求出函数的最大值,进而求出
距离.令参数部分为函数,求导,由函数的单调性求出函数的最大值,进而求出![]() 到直线
到直线![]() 的最小值.
的最小值.
解:由题意的方程可得:![]() ,
,
若直线![]() 的斜率不存在时,
的斜率不存在时,
则由题意可得![]() 的方程为:
的方程为:![]() ,
,
这时![]() 到直线
到直线![]() 的距离为2,
的距离为2,
当直线![]() 的斜率存在且不会为0时,
的斜率存在且不会为0时,
由题意的对称性设![]() ,
,
设方程为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
联立直线与椭圆的方程可得:![]() ,
,
整理可得:![]() ,
,
△![]() ,
,
即![]() ,
,![]() ,
,![]() ,
,
因为![]() 中点的横坐标为1,
中点的横坐标为1,
所以![]() ,
,
即![]()
所以![]() 到直线
到直线![]() 的距离
的距离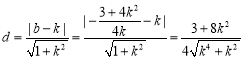
![]()
令![]() ,
,![]() ,
,
![]() ,
,
当![]() ,
,![]() ,
,![]() 单调递增,
单调递增,
当![]() ,
,![]() ,
,![]() 单调递减,
单调递减,
所以![]() 时
时![]() 最大,
最大,
且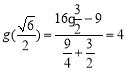 ,
,
所以![]() ,
,
故答案为:![]() .
.

【题目】3月12日,全国政协总工会界别小组会议上,人社部副部长汤涛在回应委员呼声时表示无论是从养老金方面,还是从人力资源的合理配置来说,延迟退休是大势所趋.不过,汤部长也表示,不少职工对于延迟退休有着不同的意见.某高校一社团就是否同意延迟退休的情况随机采访了200名市民,并进行了统计,得到如下的![]() 列联表:
列联表:
赞同延迟退休 | 不赞同延迟退休 | 合计 | |
男性 | 80 | 20 | 100 |
女性 | 60 | 40 | 100 |
合计 | 140 | 60 | 200 |
(1)根据上面的列联表判断能否有![]() 的把握认为对延迟退休的态度与性别有关;
的把握认为对延迟退休的态度与性别有关;
(2)为了进一步征求对延迟退休的意见和建议,从抽取的200位市民中对不赞同的按照分层抽样的方法抽取6人,再从这6人中随机抽出3名进行电话回访,求3人中至少有1人为男性的概率.
附: 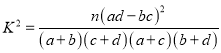 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某城市美团外卖配送员底薪是每月1800元,设每月配送单数为X,若![]() ,每单提成3元,若
,每单提成3元,若![]() ,每单提成4元,若
,每单提成4元,若![]() ,每单提成4.5元,饿了么外卖配送员底薪是每月2100元,设每月配送单数为Y,若
,每单提成4.5元,饿了么外卖配送员底薪是每月2100元,设每月配送单数为Y,若![]() ,每单提成3元,若
,每单提成3元,若![]() ,每单提成4元,小想在美团外卖和饿了么外卖之间选择一份配送员工作,他随机调查了美团外卖配送员甲和饿了么外卖配送员乙在2019年4月份(30天)的送餐量数据,如下表:
,每单提成4元,小想在美团外卖和饿了么外卖之间选择一份配送员工作,他随机调查了美团外卖配送员甲和饿了么外卖配送员乙在2019年4月份(30天)的送餐量数据,如下表:
表1:美团外卖配送员甲送餐量统计
日送餐量x(单) | 13 | 14 | 16 | 17 | 18 | 20 |
天数 | 2 | 6 | 12 | 6 | 2 | 2 |
表2:饿了么外卖配送员乙送餐量统计
日送餐量x(单) | 11 | 13 | 14 | 15 | 16 | 18 |
天数 | 4 | 5 | 12 | 3 | 5 | 1 |
(1)设美团外卖配送员月工资为![]() ,饿了么外卖配送员月工资为
,饿了么外卖配送员月工资为![]() ,当
,当![]() 时,比较
时,比较![]() 与
与![]() 的大小关系
的大小关系
(2)将4月份的日送餐量的频率视为日送餐量的概率
(ⅰ)计算外卖配送员甲和乙每日送餐量的数学期望E(X)和E(Y)
(ⅱ)请利用所学的统计学知识为小王作出选择,并说明理由.