Question

（本小题满分12分）已知椭圆M的中心为坐标原点 ，且焦点在x轴上，若M的一个顶点恰好是抛物线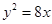的焦点，M的离心率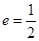，过M的右焦点F作不与坐标轴垂直的直线，交M于A，B两点。

（1）求椭圆M的标准方程；

（2）设点N（t，0）是一个动点，且，求实数t的取值范围。

 

Answer 1

【答案】

（Ⅰ）；  （Ⅱ）。

【解析】

试题分析：（Ⅰ）椭圆的标准方程：          （4分）

（Ⅱ）设，，设

     

由韦达定理得       ① （6分）

将，代入上式整理得：

，由知

，将①代入得      （10分）

所以实数    (12分)

考点：本题主要考查抛物线的几何性质，椭圆方程，直线与椭圆的位置关系，向量的坐标运算。

点评：求椭圆的标准方程是解析几何的基本问题，涉及直线与椭圆的位置关系问题，常常运用韦达定理，本题属于中档题。