题目内容
已知函数f（x）=
x2sinθ+
xcosθ，其中θ∈R，那么g（θ）=f′（1）的取值范围是
- A.[-1，1]
- B.[-2，2]
- C.[-，]
- D.[-
，]
B
分析：根据题意先求出f（x）的导数f′（x），令x=1求出f′（1）即得到g（θ），利用三角函数诱导公式转化成正弦函数求出最值得到g（θ）的范围即可．
解答：∵f（x）=x2sinθ+xcosθ，则f′（x）=xsinθ+cosθ
当x=1时，g（θ）=f′（1）=sinθ+cosθ=2（sinθ+
cosθ）=2（cos
sinθ+sincosθ）=2sin（θ+）
∵θ∈R，当
=
即
时正弦函数g（θ）达到最大，最大值等于2；
当=
即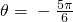
时正弦函数g（θ）达到最小，最小值等于-2．
∴g（θ）的取值范围为[-2，2]．
故答案为B
点评：本题考查学生求函数导数的能力，同时要会运用三角函数的诱导公式以及正弦函数求最大值的方法．
分析：根据题意先求出f（x）的导数f′（x），令x=1求出f′（1）即得到g（θ），利用三角函数诱导公式转化成正弦函数求出最值得到g（θ）的范围即可．
解答：∵f（x）=
x2sinθ+xcosθ，则f′（x）=xsinθ+cosθ当x=1时，g（θ）=f′（1）=sinθ+
cosθ=2（sinθ+cosθ）=2（cossinθ+sincosθ）=2sin（θ+）∵θ∈R，当
=即时正弦函数g（θ）达到最大，最大值等于2；当
=即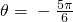时正弦函数g（θ）达到最小，最小值等于-2．∴g（θ）的取值范围为[-2，2]．
故答案为B
点评：本题考查学生求函数导数的能力，同时要会运用三角函数的诱导公式以及正弦函数求最大值的方法．
练习册系列答案
名师点拨卷系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|