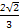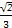题目内容
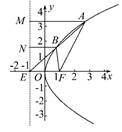
过双曲线的一个焦点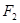 作垂直于实轴的弦
作垂直于实轴的弦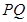 ,
, 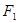 是另一焦点,若
是另一焦点,若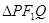 是钝角三角形,则双曲线的离心率
是钝角三角形,则双曲线的离心率 范围是( )
范围是( )
A.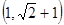 | B.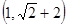 | C.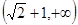 | D.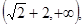 |
C
解析试题分析:根据题意,△PQF1是等腰直角三角形,且被F1F2分成两个全等的等腰直角三角形.由此结合双曲线的定义,可解出a=(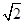 -1)c,即可得到该双曲线的离心率.
-1)c,即可得到该双曲线的离心率.
考点:求双曲线的离心率问题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
已知F是抛物线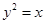 的焦点,A,B是该抛物线上的两点,
的焦点,A,B是该抛物线上的两点,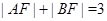 ,则线段AB的中点到y轴的距离为 ( )
,则线段AB的中点到y轴的距离为 ( )
A.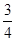 | B.1 | C.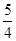 | D.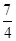 |
中心在原点的双曲线,一个焦点为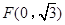 ,一个焦点到最近顶点的距离是
,一个焦点到最近顶点的距离是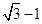 ,则双曲线的方程是( )
,则双曲线的方程是( )
A.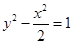 | B.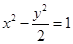 |
C.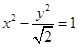 | D.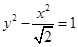 |
双曲线2x2-y2=8的实轴长是( )
| A.2 | B.2 | C.4 | D.4 |
已知F1,F2为双曲线Ax2-By2=1的焦点,其顶点是线段F1F2的三等分点,则其渐近线的方程为( )
A.y=±2 x x | B.y=±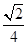 x x |
| C.y=±x | D.y=±2 x或y=± x或y=±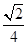 x x |
已知△ABC外接圆半径R= ,且∠ABC=120°,BC=10,边BC在x轴上且y轴垂直平分BC边,则过点A且以B,C为焦点的双曲线方程为( )
,且∠ABC=120°,BC=10,边BC在x轴上且y轴垂直平分BC边,则过点A且以B,C为焦点的双曲线方程为( )
A. - -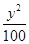 =1 =1 | B. - -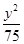 =1 =1 |
C.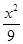 - - =1 =1 | D. - - =1 =1 |
设抛物线C:y2=4x的焦点为F,直线l过F且与C交于A,B两点.若|AF|=3|BF|,则l的方程为( )
| A.y=x-1或y=-x+1 |
B.y=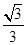 (x-1)或y=- (x-1)或y=-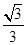 (x-1) (x-1) |
C.y= (x-1)或y=- (x-1)或y=- (x-1) (x-1) |
D.y=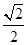 (x-1)或y=- (x-1)或y=-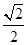 (x-1) (x-1) |
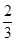 或
或
 或2
或2