题目内容
已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆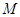 的离心率为
的离心率为 ,椭圆上异于长轴顶点的任意点
,椭圆上异于长轴顶点的任意点 与左右两焦点
与左右两焦点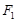 、
、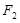 构成的三角形中面积的最大值为
构成的三角形中面积的最大值为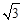 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)已知点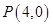 ,连接
,连接 与椭圆的另一交点记为
与椭圆的另一交点记为 ,若
,若 与椭圆相切时
与椭圆相切时 、
、 不重合,连接
不重合,连接 与椭圆的另一交点记为
与椭圆的另一交点记为 ,求
,求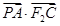 的取值范围.
的取值范围.
(1)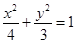 ;(2)
;(2)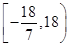 .
.
解析试题分析:(1)先利用已知条件列举出有关 、
、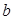 、
、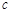 的方程组,结合三者之间满足的勾股关系求出
的方程组,结合三者之间满足的勾股关系求出 、
、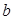 、
、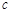 的值,从而确定椭圆的方程;(2)设直线
的值,从而确定椭圆的方程;(2)设直线 与
与 的方程分别为
的方程分别为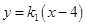 以及
以及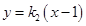 ,将两条直线方程与椭圆方程联立,结合韦达定理得到点
,将两条直线方程与椭圆方程联立,结合韦达定理得到点 与点
与点 之间的关系(关于
之间的关系(关于 轴对称),从而得到两点坐标之间的关系,最后将
轴对称),从而得到两点坐标之间的关系,最后将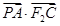 利用点
利用点 的坐标进行表示,注意到坐标的取值范围,然后利用二次函数求出
的坐标进行表示,注意到坐标的取值范围,然后利用二次函数求出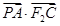 的取值范围.
的取值范围.
(1)由题可知: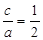 ,
,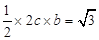 ,
,
解得: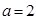 ,
, ,
,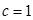 ,
,
故椭圆 的方程为:
的方程为: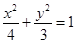 ;
;
(2)不妨设 、
、 、
、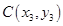 ,
,
由题意可知直线 的斜率是存在的,故设直线
的斜率是存在的,故设直线 的斜率为
的斜率为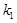 ,直线
,直线 的斜率为
的斜率为
 的方程为: 代入椭圆方程
的方程为: 代入椭圆方程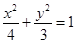 ,得
,得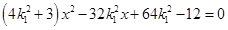 ,
, ,
,
将 ,
, 代入解得:
代入解得: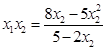 ,
, 的方程为:
的方程为: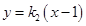 代入椭圆方程
代入椭圆方程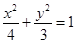 ,得
,得 ,
, ,
,
将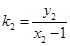 ,
, ,代入解得:
,代入解得: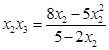 ,
, ,又
,又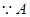 、
、 不重合,
不重合, ,
,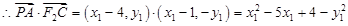
 ,
, .
.
考点:1.椭圆的方程;2.直线与椭圆的位置关系;3.二次函数;4.向量的数量积

练习册系列答案
相关题目
 (单位:万元)的关系有经验公式
(单位:万元)的关系有经验公式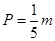 ,
, 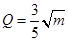 . 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资
. 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资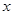 (单位:万元)
(单位:万元) (单位:万元)关于
(单位:万元)关于 是定义在
是定义在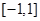 上的奇函数,且
上的奇函数,且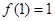 ,若
,若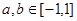 ,
,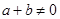 有
有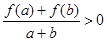 恒成立.
恒成立.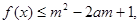 对所有
对所有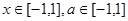 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.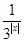 .
.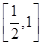 恒成立,求m的取值范围.
恒成立,求m的取值范围.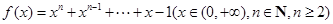 .
.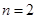 ,
,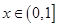 时,若不等式
时,若不等式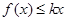 恒成立,求
恒成立,求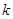 的范围;
的范围; 在
在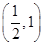 内存在零点.
内存在零点. (单位:cm)满足关系:
(单位:cm)满足关系: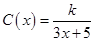 (
(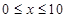 ,
,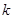 为常数),若不建隔热层,每年能源消耗费用为8万元.设
为常数),若不建隔热层,每年能源消耗费用为8万元.设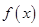 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.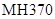 残骸,我国“雪龙号”科考船于2014年3月26日从港口
残骸,我国“雪龙号”科考船于2014年3月26日从港口 出发,沿北偏东
出发,沿北偏东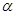 角的射线
角的射线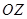 方向航行,而在港口北偏东
方向航行,而在港口北偏东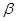 角的方向上有一个给科考船补给物资的小岛
角的方向上有一个给科考船补给物资的小岛 ,
,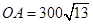 海里,且
海里,且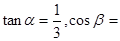
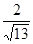 .现指挥部需要紧急征调位于港口
.现指挥部需要紧急征调位于港口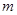 海里的
海里的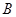 处的补给船,速往小岛
处的补给船,速往小岛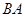 方向全速追赶科考船,并在
方向全速追赶科考船,并在 处相遇.经测算当两船运行的航线与海岸线
处相遇.经测算当两船运行的航线与海岸线 围成的三角形
围成的三角形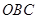 的面积
的面积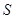 最小时,这种补给方案最优.
最小时,这种补给方案最优.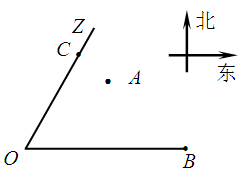
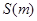 ;
; 的图象关于坐标原点对称。
的图象关于坐标原点对称。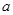 的值,并求出函数
的值,并求出函数 的零点;
的零点; 在[0,1]内存在零点,求实数b的取值范围;
在[0,1]内存在零点,求实数b的取值范围;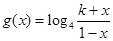 ,已知
,已知 的反函数
的反函数 =
= ,若不等式
,若不等式 在
在 上恒成立,求满足条件的最小整数k的值。
上恒成立,求满足条件的最小整数k的值。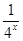 -
-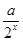 (a∈R).
(a∈R).