题目内容
【题目】函数![]() 其图像与
其图像与![]() 轴交于
轴交于![]() 两点,且
两点,且![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)证明:![]() ;(
;(![]() 为
为![]() 的导函数;)
的导函数;)
(3)设点C在函数![]() 图像上,且△ABC为等腰直角三角形,记
图像上,且△ABC为等腰直角三角形,记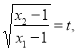 求
求![]() 的值.
的值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)![]() ,当
,当![]() 时,函数单调递增,不符合题意;当
时,函数单调递增,不符合题意;当![]() 时,要函数图像与
时,要函数图像与![]() 轴有两个交点,则需要极小值小于零且区间端点函数值大于零,由此可求得
轴有两个交点,则需要极小值小于零且区间端点函数值大于零,由此可求得![]() ;(2)先将
;(2)先将![]() 两点的坐标代入函数中,求出
两点的坐标代入函数中,求出![]() 的值,然后求出
的值,然后求出![]() 的表达式,利用导数证明这个表达式是单调递减的,由此可证明
的表达式,利用导数证明这个表达式是单调递减的,由此可证明![]() ;(3)根据已知条件有
;(3)根据已知条件有![]() ,利用等腰三角形求出
,利用等腰三角形求出![]() 的坐标,代入函数解析式,化简后求得
的坐标,代入函数解析式,化简后求得![]() .
.
试题解析:
(1)![]()
![]() ,
,![]()
![]() ,
,
若![]() ,则
,则![]() ,则函数
,则函数![]() 是单调增函数,这与题设矛盾.
是单调增函数,这与题设矛盾.
![]() ,令
,令![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,
,![]() 单调减,
单调减,
当![]() 时,
时,![]() ,
,![]() 是单调增函数,于是当
是单调增函数,于是当![]() 时,
时,![]() 取得极小值,
取得极小值,
![]() 函数
函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() ,
,
![]() ,即
,即![]() ,此时,存在
,此时,存在![]() ,
,![]() ,存在
,存在![]() , =a3﹣3alna+a
, =a3﹣3alna+a![]() ,又由
,又由![]() 在
在![]() 及
及![]() 上的单调性及曲线在
上的单调性及曲线在![]() 上不间断,可知
上不间断,可知![]() 为所求取值范围.
为所求取值范围.
(2)![]()
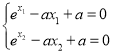 ,
,![]() 两式相减得
两式相减得![]() .记
.记![]() (
(![]() ),
),
则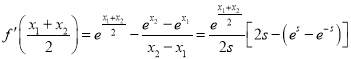 ,
,
设![]() 则
则![]() ,
,![]()
![]() 是单调减函数,
是单调减函数,
则有![]() ,而
,而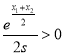 ,
,![]()
![]() .
.
又![]() 是单调增函数,且
是单调增函数,且![]()
![]()
![]() .
.
(3)依题意有![]() ,则
,则![]() ,
,![]() .
.
于是![]() ,在等腰三角形
,在等腰三角形![]() ,显然
,显然![]() ,
,![]()
![]() ,即
,即![]() ,由直角三角形斜边的中线性质,可知
,由直角三角形斜边的中线性质,可知![]() ,
,![]()
![]() ,即
,即![]() ,
,
![]()
![]() ,
,
即![]()
![]()
![]() ,则
,则 ,又
,又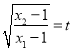 ,
,
![]()
![]() ,即
,即![]() ,
,![]()
![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目