题目内容
判断下列函数的奇偶性，并证明：
（1）
（2）f（x）=x4-1．
解：（1）为奇函数，（2）f（x）=x4-1为偶函数．
证明：（1）∵x≠0∴的定义域为{x|x≠0}，
又f（-x）=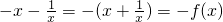
∴为奇函数；
（2）∵）f（x）=x4-1的定义域为R，
f（-x）=（-x）4-1=f（x），
∴f（x）=x4-1为偶函数．
分析：先考查函数的定义域是否关于原点对称，满足后再用奇偶函数的定义判断即可．
点评：本题考查函数奇偶性的判断，关键是理解并应用好奇偶函数的定义，属于基础题．
为奇函数，（2）f（x）=x4-1为偶函数．证明：（1）∵x≠0∴
的定义域为{x|x≠0}，又f（-x）=
∴
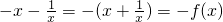
为奇函数；（2）∵）f（x）=x4-1的定义域为R，
f（-x）=（-x）4-1=f（x），
∴f（x）=x4-1为偶函数．
分析：先考查函数的定义域是否关于原点对称，满足后再用奇偶函数的定义判断即可．
点评：本题考查函数奇偶性的判断，关键是理解并应用好奇偶函数的定义，属于基础题．
练习册系列答案
口算能手系列答案
相关题目