题目内容
曲线
在点
处的切线斜率为（ ）
A.
1 B. 2 C. 
D. 
【答案】
C
【解析】解：因为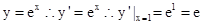
，利用导数的几何意义可知导数值即为该点的切线斜率。
练习册系列答案
怎样学好牛津英语系列答案
相关题目
怎样学好牛津英语系列答案题目内容
曲线在点处的切线斜率为（ ）
A.
1 B. 2 C. D.
C
【解析】解：因为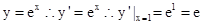，利用导数的几何意义可知导数值即为该点的切线斜率。
怎样学好牛津英语系列答案
（
是自然对数的底数）（Ⅰ）若对于任意
恒成立，试确定实数
的取值范围；(Ⅱ)当
时，是否存在
，使曲线
在点
处的切线斜率与
在
上的最小值相等？若存在，求符合条件的
的个数；若不存在，请说明理由.
（
是自然对数的底数）.
在
处的切线也是抛物线
的切线，求
的值；
恒成立，试确定实数
时，是否存在
，使曲线
在点
处的切线斜率与
在
上的最小值相等？若存在，求符合条件的
的个数；若不存在，请说明理由.
.
与直线
垂直的切线方程；
使曲线
在
点处的切线斜率为
,且
,求实数
的取值范围.
在点
处的切线斜率为
▲ . 
在点
处的切线斜率为
的极值；
在（-∞，1）上是增函数，求实数
的取值范围；
满足
，求证：对一切