题目内容
【题目】已知平面向量a＝(1，x)，b＝(2x＋3，－x)，x∈R.
(1)若a⊥b，求x的值；
(2)若a∥b，求|a－b|的值．
【答案】（1）x＝－1或x＝3（2）2或2
.
【解析】(1)若a⊥b，
则a·b＝(1，x)·(2x＋3，－x)＝1×(2x＋3)＋x(－x)＝0，
整理得x2－2x－3＝0，解得x＝－1或x＝3.
(2)若a∥b，则有1×(－x)－x(2x＋3)＝0，
即x(2x＋4)＝0，解得x＝0或x＝－2.
当x＝0时，a＝(1，0)，b＝(3，0)，a－b＝(－2，0)，
∴|a－b|＝
＝2；
当x＝－2时，a＝(1，－2)，b＝(－1，2)，a－b＝(2，－4)，
∴|a－b|＝
＝2
.
综上，可知|a－b|＝2或2.
练习册系列答案
相关题目
【题目】为了分析某个高三学生的学习状态，对其下一阶段的学习提供指导性建议．现对他前7次考试的数学成绩
、物理成绩
进行分析．下面是该生7次考试的成绩．
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
（1）他的数学成绩与物理成绩哪个更稳定？请给出你的证明；
（2）已知该生的物理成绩与数学成绩是线性相关的，若该生的物理成绩达到115分，请你估计他的数学成绩大约是多少？并请你根据物理成绩与数学成绩的相关性，给出该生在学习数学、物理上的合理建议．
参考公式：方差公式：
，其中
为样本平均数.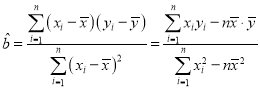
，
。
