题目内容
20.当实数k变化时,对于方程(2|x|-1)2-(2|x|-1)-k=0的解的判断不正确的是( )| A. | $k<-\frac{1}{4}$时,无解 | B. | $k=-\frac{1}{4}$时,有2个解 | ||
| C. | $-\frac{1}{4}<k≤0$时,有4个解 | D. | k>0时,有2个解 |
分析 令令t=2|x|-1,则t∈[0,+∞),方程即k=t2-t∈[-$\frac{1}{4}$,+∞),再利用二次函数的性质判断各个选项是否正确,从而得出结论.
解答 解:令t=2|x|-1,则t∈[0,+∞),
方程即 t2-t-k=0,即 k=t2-t.
由于t2-t=(t-$\frac{1}{2}$)2-$\frac{1}{4}$≥-$\frac{1}{4}$,
当t=$\frac{1}{2}$时,取得最小值-$\frac{1}{4}$,
当k<-$\frac{1}{4}$时,方程无解,故A正确;
当k=-$\frac{1}{4}$时,方程有两解,且为x=±log2$\frac{3}{2}$,故B正确;
当k>0时,方程t2-t-k=0的判别式△=1+4k>0,两根异号,
则方程有两解,故D正确;
当k=0时,方程即为t2-t=0,求得t=0,或t=1,
此时x=0或±1,有三个解,故C不正确.
故选C.
点评 本题主要考查方程根的存在性及个数的判断,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
12.下列函数中,既是定义域上的奇函数又在区间(0,1)内单调递增的是( )
| A. | $y=x+\frac{1}{x}$ | B. | y=xsinx+cosx | C. | $y={e^x}-\frac{1}{e^x}$ | D. | $y=ln\frac{1-x}{1+x}$ |
10.执行如图所示的程序框图,若x=4,则输出的y=( )


| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
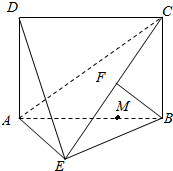 如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC,F为CE上的点,且BF⊥平面ACE.
如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC,F为CE上的点,且BF⊥平面ACE.