题目内容
已知x1,x2∈(0,+∞),且x1≠x2,则下列满足
>f(
)的函数序号为
①f(x)=x2
②f(x)=ex
③f(x)=lnx
④f(x)=
⑤f(x)=
.
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
①②⑤
①②⑤
(把满足要求的序号都写上)①f(x)=x2
②f(x)=ex
③f(x)=lnx
④f(x)=
| x |
⑤f(x)=
| 1 |
| x |
分析:满足条件
>f(
)的函数为凹函数,利用数形结合进行判断即可.
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
解答: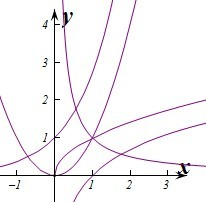 解:由函数图象可知,满足条件
解:由函数图象可知,满足条件
>f(
)的函数为凹函数,
分别作出函数对应的图象,由图象可知,满足条件的函数是:
①f(x)=x2
②f(x)=ex
⑤f(x)=
.
③④为凸函数满足
<f(
).
故答案为:①②⑤
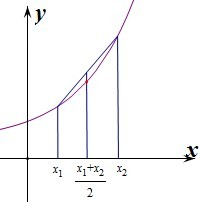
 解:由函数图象可知,满足条件
解:由函数图象可知,满足条件| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
分别作出函数对应的图象,由图象可知,满足条件的函数是:
①f(x)=x2
②f(x)=ex
⑤f(x)=
| 1 |
| x |
③④为凸函数满足
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
故答案为:①②⑤

点评:本题主要考查函数的图象和性质,利用数形结合是解决此类问题的基本方法,要求熟练掌握满足
>f(
)的函数为凹函数,满足
<f(
)的函数为凸函数.
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
定义在R上的函数y=f(x)满足f(5+x)=f(-x),(x-
)f′(x)>0,已知x1<x2,则f(x1)>f(x2)是x1+x2<5的( )条件.
| 5 |
| 2 |
| A、充分不必要 |
| B、必要不充分 |
| C、充分必要 |
| D、既不充分也不必要 |