题目内容

在矩形ABCD中,|AB|=2
,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且
==.
(Ⅰ)求证:直线ER与GR′的交点P在椭圆Ω:
+y
2=1上;
(Ⅱ)若M、N为椭圆Ω上的两点,且直线GM与直线GN的斜率之积为
,求证:直线MN过定点;并求△GMN面积的最大值.
分析:(I)利用已知可得直线GR′,ER的方程,利用即可得出点P的坐标,代入满足椭圆Ω的方程即可;
(II)当直线MN的斜率存在时,设MN的方程为y=kx+b,M(x
1,y
1),N(x
2,y
2).与椭圆的方程联立即可得到根与系数的关系,再利用k
GM•k
GN=
.即可得出b的值,从而证明直线过定点,再利用弦长公式和点到直线的距离公式即可得到三角形的面积计算公式,通过换元利用基本不等式即可得出.
解答:解:(Ⅰ)∵
==,∴
R(,0),
R′(,1-).
又n>0,则直线GR'的方程为
y=-x+1①
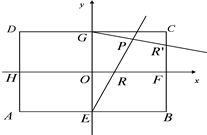
又E(0,-1)则直线ER的方程为
y=x-1②
由①②得
P(,)∵|OP|
2=
+()2==1∴直线MN与MN的交点MN在椭圆
Ω:+y2=1上.
(Ⅱ)①当直线MN的斜率不存在时,设MN:x=t
(-<t<).
不妨取
M(t,),N
(t,-),∴
kGM•kGN=,不合题意.
②当直线MN的斜率存在时,设MN的方程为y=kx+b,M(x
1,y
1),N(x
2,y
2).

联立方程
得(1+3k
2)x
2+6kbx+3b
2-3=0
则△=12(3k
2-b
2+1)>0,
∴
x1+x2=,x1•x2=.
又k
GM•k
GN=
•=
| k2x1x2+k(b-1)(x1+x2)+(b-1)2 |
| x1x2 |
=
.
即
(3k2-2)x1x2+3k(b-1)(x1+x2)+3(b-1)2=0将
x1+x2=,x1•x2=代入上式得b
2+2b-3=0
解得b=-3或b=1(舍)
∴直线过定点(0,3).
∵
|MN|=|x1-x2|,点G到直线MN的距离为
d=∴
S△GMN=|MN|•d=2|x1-x2|=2=4•由b=-3及△>0知:3k
2-8>0,令
=t>0 即3k
2=t
2+8.
∴
==≤ 当且仅当t=3时,
S
△GMN=
.
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式、基本不等式等基础知识与基本技能方法,属于难题.
练习册系列答案
相关题目
 在矩形ABCD中,|AB|=2
在矩形ABCD中,|AB|=2 又E(0,-1)则直线ER的方程为y=
又E(0,-1)则直线ER的方程为y=
 又E(0,-1)则直线ER的方程为y=
又E(0,-1)则直线ER的方程为y=

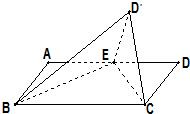 如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.
如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.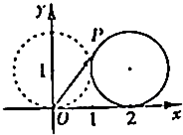 (1)如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,
(1)如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,