题目内容

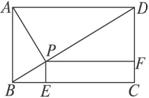
在矩形ABCD中，AB=2，AD=1，E为BC的中点，F在边CD上，
AB
•
AF
=
2
，则
AE
•
BF
=
 
．
分析：根据所给的图形，把已知向量用矩形的边所在的向量来表示，做出要用的向量的模长，表示出要求得向量的数量积，注意应用垂直的向量数量积等于0，得到结果．
解答：解：由题意可得，
AF
=
AD
+
DF
 
AE
，=
AB
+
BE
，
BF
=
BC
+
CF
，且
AB
⊥
BC
，
BE
⊥
CF
．
∵
AB
•
AF
=
AB
•（
AD
+
DF
）=0+
AB
•
DF
=|
AB
|•|
DF
|=2|
DF
|=
2
，∴|
DF
|=
2
2
．
又∵
AE
•
BF
=（
AB
+
BE
）•（
BC
+
CF
）=0+
AB
•
CF
+
BE
•
BC
+0=-|
AB
|•|
CF
|+|
BE
|•|
BC
|
=-2（2-|
DF
|）+
1
2
×1=-4+2×
2
2
+
1
2
=-
7
2
+
2
，
故答案为-
7
2
+
2
．
点评：本题考查平面向量的数量积的运算，两个向量的加减法的法则，以及其几何意义，解题的关键是把要用的向量表示成已知向量的和的形式，属于中档题目．
练习册系列答案
相关题目
如图，在矩形ABCD中，AB=3
3
，BC=3，沿对角线BD将BCD折起，使点C移到点C′，且C′在平面ABD的射影O恰好在AB上
（1）求证：BC′⊥面ADC′；
（2）求二面角A-BC′-D的正弦值．
如图，在矩形ABCD中，已知AD=2，AB=a（a＞2），E、F、G、H分别是边AD、AB、BC、CD上的点，若AE=AF=CG=CH，问AE取何值时，四边形EFGH的面积最大？并求最大的面积．

如图，已知在矩形ABCD中，A(－4，4)、D(5，7)，其对角线的交点E在第一象限内且与y轴的距离为一个单位，动点P(x，y)沿矩形一边BC运动，求的取值范围．
如图1-5-5,在矩形ABCD中,过A作对角线BD的垂线AP与BD交于P,过P作BC、CD的垂线PE、PF,分别与BC、CD交于E、F.

图1-5-5

求证:AP3=BD·PE·PF.

如图所示,已知在矩形ABCD中,||=.设=a, =b, =c,求|a+b+c|.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网