题目内容
已知f(x)=x|x-a|-2。
(1)当a=1时,解不等式f(x)<|x-2|;
(2)当x∈(0,1]时,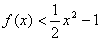 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
(1)当a=1时,解不等式f(x)<|x-2|;
(2)当x∈(0,1]时,
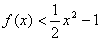 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。解:(1)a=1时,f(x)<|x-2|,
即x|x-1|-2<|x-2|(*)
①当x≥2时,由(*)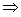 x(x-1)-2<x-2
x(x-1)-2<x-2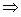 0<x<2
0<x<2
又x≥2,
∴x∈ ;
;
②当1≤x<2时,
由(*)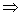 x(x-1)-2<2-x
x(x-1)-2<2-x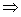 -2<x<2
-2<x<2
又1≤x<2,
∴1≤x<2;
③当x<1时,
由(*)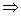 x(1-x)-2<2-x
x(1-x)-2<2-x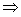 x∈R
x∈R
又x<1,
∴x<1
综上:由①②③知原不等式的解集为{x|x<2}。
(2)当x∈(0,1]时,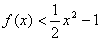
即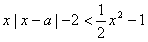 恒成立,
恒成立,
也即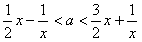 在x∈(0,1]上恒成立,
在x∈(0,1]上恒成立,
而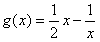 在(0,1]上为增函数,
在(0,1]上为增函数,
故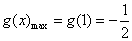 ,
,
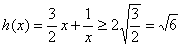 ,当且仅当
,当且仅当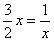
即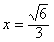 时,等号成立
时,等号成立
故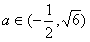 。
。
即x|x-1|-2<|x-2|(*)
①当x≥2时,由(*)
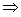 x(x-1)-2<x-2
x(x-1)-2<x-2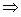 0<x<2
0<x<2又x≥2,
∴x∈
 ;
; ②当1≤x<2时,
由(*)
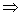 x(x-1)-2<2-x
x(x-1)-2<2-x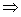 -2<x<2
-2<x<2 又1≤x<2,
∴1≤x<2;
③当x<1时,
由(*)
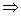 x(1-x)-2<2-x
x(1-x)-2<2-x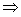 x∈R
x∈R 又x<1,
∴x<1
综上:由①②③知原不等式的解集为{x|x<2}。
(2)当x∈(0,1]时,
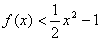
即
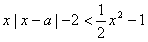 恒成立,
恒成立,也即
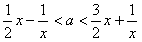 在x∈(0,1]上恒成立,
在x∈(0,1]上恒成立,而
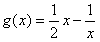 在(0,1]上为增函数,
在(0,1]上为增函数,故
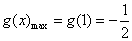 ,
,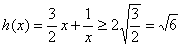 ,当且仅当
,当且仅当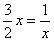
即
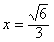 时,等号成立
时,等号成立故
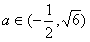 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由.