题目内容
如图24,已知ABCD是矩形纸片,E是AB上一点,BE∶EA =5∶3,EC=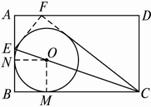
图24
(1)求AB、BC的长度各是多少;
(2)若⊙O内切于以F、E、B、C为顶点的四边形,求⊙O的面积.
思路分析:考察所给的条件,翻折△BCE,则△CBE≌△CFE,这样图形中提供了很多的线段相等、角相等.
解:(1)连结CE、CF、EF,设BE =5x,EA =3x.?
∵四边形ABCD是矩形,?
∴AB =CD =8x,AD =BC,∠B =∠A =∠D =90°.?
∵△CBE≌△CFE,?
∴EF =5x,FC=BC,?∠CFE =90°.??
∵∠AEF +∠EFC+∠DFC=180°,?
∴∠AFE +∠DFC=90°.?
又∵∠AEF +∠AFE =90°,∠AEF =∠DFC,?
∴sin∠AEF =sin∠DFC,即![]() =
=![]() .?
.?
∴![]() =
=![]() ,则FC =10x.?
,则FC =10x.?
∴![]() =
=![]() =
=![]() .?
.?
∴x =3.∴AB =24,BC =30.?

(2)∵CE平分∠FCB和∠FEB,∴O在EC上.?
设⊙O和BC切于M,和AB切于N,连结OM、ON,设⊙O的半径为r,?
∴OM⊥BC,ON⊥AB.∴OM∥AB,ON∥BC.?
∴OM =BN =ON =BM =r.?
∴![]() =
=![]() ,即
,即![]() =
=![]() .∴r =10.?
.∴r =10.?
∴⊙O的面积为100π.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
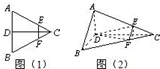 已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC边上的点,且满足
已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC边上的点,且满足
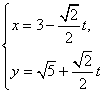 (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为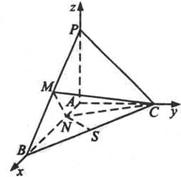 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,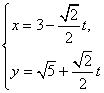 (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为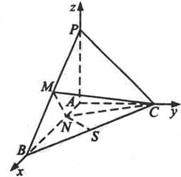 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,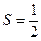 AD·AE,求∠BAC的大小。
AD·AE,求∠BAC的大小。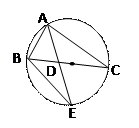
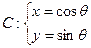
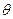 为参数且(0≤
为参数且(0≤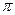 )
)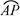 P为半圆C上一点,A(1,0)O为坐标原点,点M在射线OP上,线段OM与 的长度均为
P为半圆C上一点,A(1,0)O为坐标原点,点M在射线OP上,线段OM与 的长度均为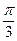 。
。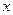 轴为正半轴为极轴建立极坐标系求点M的极坐标。
轴为正半轴为极轴建立极坐标系求点M的极坐标。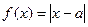
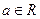
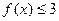 的解集为
的解集为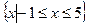 求a值。
求a值。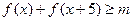 对一切实数
对一切实数