题目内容
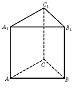
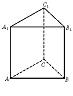
 已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC边上的点,且满足
已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC边上的点,且满足| CE |
| CA |
| CF |
| CB |
(Ⅰ)试判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(Ⅱ)求二面角B-AC-D的大小;
(Ⅲ)若异面直线AB与DE所成角的余弦值为
| ||
| 4 |
分析:(I)由题意,有线段长成比例利用线面平行的判定定理即可得证;
(II)由题意利用二面角平面角的概念,在三角形中利用面积相等及解三角形求出二面角的大小;
(III)利用方程的思想,利用异面直线的所成角的大小,进而解出变量的大小.
(II)由题意利用二面角平面角的概念,在三角形中利用面积相等及解三角形求出二面角的大小;
(III)利用方程的思想,利用异面直线的所成角的大小,进而解出变量的大小.
解答: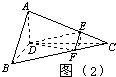 解:(Ⅰ)AB∥平面DEF.在△ABC中,
解:(Ⅰ)AB∥平面DEF.在△ABC中,
∵E、F分别是AC、BC上的点,且满足
=
=k,
∴AB∥EF.
∵AB?平面DEF,EF?平面DEF,∴AB∥平面DEF
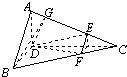 (Ⅱ)过D点作DG⊥AC于G,连接BG,
(Ⅱ)过D点作DG⊥AC于G,连接BG,
∵AD⊥CD,BD⊥CD,
∴∠ADB是二面角A-CD-B的平面角.
∴∠ADB=90°,即BD⊥AD.
∴BD⊥平面ADC.∴BD⊥AC.
∴AC⊥平面BGD.∴BG⊥AC.
∴∠BGD是二面角B-AC-D的平面角.
在ADC中,AD=a,DC=
a,AC=2a,
∴DG=
=
=
.
在Rt△BDG中,tan∠BGD=
=
.
∴∠BGD=arctan
.
即二面角B-AC-D的大小为arctan
.
(Ⅲ)∵AB∥EF,∴∠DEF(或其补角)是异面直线AB与DE所成的角.
∵AB=
a,∴EF=
ak.
又DC=
a,CE=kCA=2ak,
∴DF=DE=
=
=
=a
.
∴cos∠DEF=
=
=
.
∴2
ak=
•a
.解得k=
.
 解:(Ⅰ)AB∥平面DEF.在△ABC中,
解:(Ⅰ)AB∥平面DEF.在△ABC中,∵E、F分别是AC、BC上的点,且满足
| CE |
| CA |
| CF |
| CB |
∴AB∥EF.
∵AB?平面DEF,EF?平面DEF,∴AB∥平面DEF
 (Ⅱ)过D点作DG⊥AC于G,连接BG,
(Ⅱ)过D点作DG⊥AC于G,连接BG,∵AD⊥CD,BD⊥CD,
∴∠ADB是二面角A-CD-B的平面角.
∴∠ADB=90°,即BD⊥AD.
∴BD⊥平面ADC.∴BD⊥AC.
∴AC⊥平面BGD.∴BG⊥AC.
∴∠BGD是二面角B-AC-D的平面角.
在ADC中,AD=a,DC=
| 3 |
∴DG=
| AD•DC |
| AC |
| ||
| 2a |
| ||
| 2 |
在Rt△BDG中,tan∠BGD=
| BD |
| DG |
2
| ||
| 3 |
∴∠BGD=arctan
2
| ||
| 3 |
即二面角B-AC-D的大小为arctan
2
| ||
| 3 |
(Ⅲ)∵AB∥EF,∴∠DEF(或其补角)是异面直线AB与DE所成的角.
∵AB=
| 2 |
| 2 |
又DC=
| 3 |
∴DF=DE=
| DC2+CE2-2DC•CE•cos∠ACD |
3a2+4a2k2-2
|
| 3a2+4a2k2-6a2k |
| 3+4k2-6k |
∴cos∠DEF=
| DE2+EF2-DF2 |
| 2DE•EF |
| EF |
| 2DE |
| ||
| 4 |
∴2
| 2 |
| 2 |
| 3+4k2-6k |
| 1 |
| 2 |
点评:此题重点考查了利用线段成比例去进行判定线面平行,还考查了二面角的平面角的概念及利用方程的思想借助异面直线所成角的大小建立方程进而求解变量的值.

练习册系列答案
相关题目
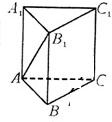 如图,在正三棱柱ABC-A1B1C1中,已知BB1=BC=2.
如图,在正三棱柱ABC-A1B1C1中,已知BB1=BC=2. 已知正三棱柱ABC-A1B1C1,底面边长AB=2,AB1⊥BC1,点O、O1分别是边AC,A1C1的中点,建立如图所示的空间直角坐标系.
已知正三棱柱ABC-A1B1C1,底面边长AB=2,AB1⊥BC1,点O、O1分别是边AC,A1C1的中点,建立如图所示的空间直角坐标系.