题目内容
将正确答案填在答卷相应的位置上)已知平面向量| a |
| b |
| c |
| a |
| a |
| b |
| b |
| a |
| c |
分析:利用作弊哦啊形式的运算求出
•
,进而求出
,分别用坐标形式和定义求出
•
,由两种方式求得的结果相同,求出cosθ (cosθ为所求)的值.
| a |
| b |
| c |
| a |
| c |
解答:解:设
与
夹角为θ,∵
•
=(1,2)•(-1,3)=-1+6=5,
∴
=
-(
•
)
=(1,2)-5(-1,3)=(6,-13),
由
•
=(1,2)•(6,-13)=6-26=-20=|
|•|
|cosθ
=
×
•
cosθ 得:
cosθ=-
,
故答案为-
.
| a |
| c |
| a |
| b |
∴
| c |
| a |
| a |
| b |
| b |
由
| a |
| c |
| a |
| c |
=
| 5 |
| 5 |
| 41 |
cosθ=-
4
| ||
| 41 |
故答案为-
4
| ||
| 41 |
点评:本题考查两个向量的数量积的定义和坐标形式的运算公式,待定系数法求出两个向量的夹角的余弦值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
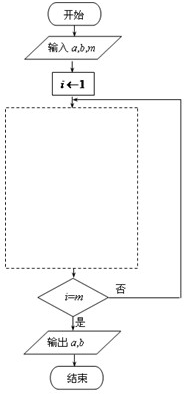 若数列{an},{bn}中,a1=a,b1=b,
若数列{an},{bn}中,a1=a,b1=b,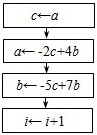 B、
B、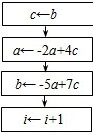
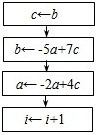 D、
D、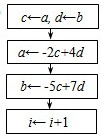
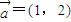 ,
,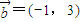 ,
,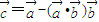 ,则
,则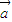 与
与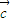 夹角的余弦值为 .
夹角的余弦值为 .