题目内容
给出问题:F1、F2是双曲线![]() =1的焦点,点P在双曲线上,若点P到焦点F1的距离等于9,求点P到焦点F2的距离.
=1的焦点,点P在双曲线上,若点P到焦点F1的距离等于9,求点P到焦点F2的距离.
某学生的解答如下:
双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.
该学生的解答是否正确?若正确,请将他的解题依据填在下面空格内;若不正确,将正确答案填在下面空格内________.
答案:
解析:
解析:
|
答案:|PF2|=17 解析:在双曲线的定义中,||PF1|-|PF2||=2a,即|PF1|-|PF2|=±2a,正负号的取舍取决于P点的位置是在左支上还是在右支上. ∵|F1F2|=12,|PF1|=9,∴|PF2|=17. 若|PF2|=1,这与三角形两边之差小于第三边矛盾. |

练习册系列答案
相关题目
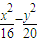 =1的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P到焦点F2的距离.某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.
=1的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P到焦点F2的距离.某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.