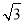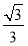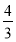题目内容
已知函数f(x)=Msin(ωx+φ)(M>0,ω>0,|φ|< )的部分图象如图所示.
)的部分图象如图所示.

(1)求函数f(x)的解析式;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,若(2a-c)cos B=bcos C,求f 的取值范围.
的取值范围.
(1)f(x)=sin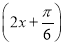 (2)
(2)
【解析】(1)由图象知M=1,
f(x)的最小正周期T=4×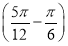 =π,故ω=
=π,故ω= =2.
=2.
将点 代入f(x)的解析式得sin
代入f(x)的解析式得sin =1,
=1,
即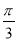 +φ=2kπ+
+φ=2kπ+ ,φ=2kπ+
,φ=2kπ+ ,k∈Z,又|φ|<
,k∈Z,又|φ|<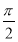 ∴φ=
∴φ= .
.
故函数f(x)的解析式为f(x)=sin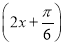 .
.
(2)由(2a-c)cos B=bcosC,得(2sin A-sin C)cos B=sin Bcos C,
∴2sin Acos B=sin(B+C)=sin A.
∵sin A≠0,∴cos B= ,∴B=
,∴B= ,∴A+C=
,∴A+C=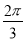 .
.
∵f =sin
=sin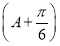 ,又∵0<A<
,又∵0<A<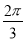 ,∴A+
,∴A+ ∈
∈ .
.
∴sin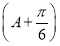 ∈
∈ ,∴f
,∴f ∈
∈ .
.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目