题目内容
【题目】已知定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,且
,且![]() 的导函数
的导函数![]() ,则不等式
,则不等式![]() 的解集为( )
的解集为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 或
或![]()
【答案】C
【解析】分析:根据题意,设g(x)=f(x)﹣2x2+x﹣1,由题设可知g′(x)<0,即函数g(x)在R上为减函数,则原不等式可以转化为g(x)<g(3),结合函数的单调性分析可得答案.
详解:根据题意,设g(x)=f(x)﹣2x2+x﹣1,其导数g′(x)=f′(x)﹣4x+1,
又由f'(x)<4x﹣1,即f′(x)﹣4x+1<0,
则g′(x)<0,即函数g(x)在R上为减函数,
又由f(3)=16,则g(3)=f(3)﹣18+3﹣1=0,
f(x)<2x2﹣x+1f(x)﹣2x2+x﹣1<0g(x)<g(3),
又由函数g(x)为减函数,则有x>3,
则不等式f(x)<2x2﹣x+1的解集为{x|x>3};
故选:C.

 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
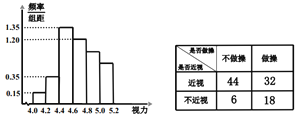
轻巧夺冠周测月考直通高考系列答案【题目】眼保健操是一种眼睛的保健体操,主要是通过按摩眼部穴位,调整眼及头部的血液循环,调节肌肉,改善眼的疲劳,达到预防近视等眼部疾病的目的.某学校为了调查推广眼保健操对改善学生视力的效果,在应届高三的全体800名学生中随机抽取了100名学生进行视力检查,并得到如图的频率分布直方图.
(1)若直方图中后三组的频数成等差数列,试估计全年级视力在5.0以上的人数;
(2)为了研究学生的视力与眼保健操是否有关系,对年级不做眼保健操和坚持做眼保健操的学生进行了调查,得到下表中数据,根据表中的数据,能否在犯错的概率不超过0.005的前提下认为视力与眼保健操有关系?
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取8人,进一步调查他们良好的护眼习惯,在这8人中任取2人,记坚持做眼保健操的学生人数为X,求X的分布列和数学期望.
附:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
【题目】近年来,国资委.党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:
土地使用面积 | 1 | 2 | 3 | 4 | 5 |
管理时间 | 8 | 10 | 13 | 25 | 24 |
并调查了某村300名村民参与管理的意愿,得到的部分数据如下表所示:
愿意参与管理 | 不愿意参与管理 | |
男性村民 | 150 | 50 |
女性村民 | 50 |
(1)求出相关系数![]() 的大小,并判断管理时间
的大小,并判断管理时间![]() 与土地使用面积
与土地使用面积![]() 是否线性相关?
是否线性相关?
(2)是否有99.9%的把握认为村民的性别与参与管理的意愿具有相关性?
(3)若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取3人,记取到不愿意参与管理的男性村民的人数为![]() ,求
,求![]() 的分布列及数学期望。
的分布列及数学期望。
参考公式:
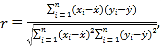
![]()
其中![]() 。临界值表:
。临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考数据:![]()
【题目】1772年德国的天文学家波得发现了求太阳的行星距离的法则,记地球距离太阳的平均距离为10,可以算得当时已知的六大行星距离太阳的平均距离如下表:
星名 | 水星 | 金星 | 地球 | 火星 | 木星 | 土星 |
与太阳的距离 | 4 | 7 | 10 | 16 | 52 | 100 |
除水星外,其余各星与太阳的距离都满足波得定则(某一数列规律),当时德国数学家高斯根据此定则推算,火星和木星之间距离太阳28还有一颗大行星,1801年,意大利天文学家皮亚齐经过观测,果然找到了火星和木星之间距离太阳28的谷神星以及它所在的小行星带,请你根据这个定则,估算从水星开始由近到远算,第10个行星与太阳的平均距离大约是( )
A.388B.772C.1540D.3076
【题目】(2017·全国卷Ⅲ文,18)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.