题目内容
4.已知数列{an}满足a1=3,an+1=2an-n+1(n∈N*).(1)若bn=an-n(n∈N*),求证数列{bn}成等比数列;
(2)设数列{an}的前n项之和为Sn,求Sn.
分析 (1)由已知得an+1-(n+1)=2an-n+1-n-1=2(an-n),由此能证明数列{bn}成等比数列.
(2)由${b}_{n}={a}_{n}-n={2}^{n}$,得${a}_{n}={2}^{n}+n$,由此利用公组求和法能求出数列{an}的前n项之和.
解答 证明:(1)∵{an}满足a1=3,an+1=2an-n+1(n∈N*).
∴an+1-(n+1)=2an-n+1-n-1=2(an-n),(n∈N*)
∵bn=an-n(n∈N*),a1-1=2,
∴数列{bn}成以2为首项,以2为公比的等比数列.
(2)由(1)得${b}_{n}={a}_{n}-n={2}^{n}$,
∴${a}_{n}={2}^{n}+n$,
∴Sn=(2+22+…+2n)+(1+2+3+…+n)
=$\frac{2(1-{2}^{n})}{1-2}$+$\frac{n(n+1)}{2}$
=${2}^{n+1}-2+\frac{n(n+1)}{2}$.
点评 本题考查等比数列的证明,考查数列的通项公式的求法,是中档题,解题时要认真审题,注意构造法和分组求和法的合理运用.

练习册系列答案
相关题目
19.已知正方体ABCD-A1B1C1D1中的棱长为8,点H在棱AA1上,且HA1=2,点E、F分别为棱B1C1、C1C的中点,P是侧面BCC1B1内一动点,且满足PE⊥PF,则当点P运动时,HP2的最小值是( )
| A. | 10 | B. | 27-6$\sqrt{2}$ | C. | 2$\sqrt{21}$ | D. | 108-24$\sqrt{2}$ |
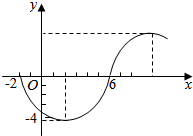 函数f(x)=Asin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示.