题目内容
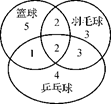
在高中“自选模块”考试中,某考场的每位同学都选了一道数学题,第一小组选《数学史与不等式选讲》的有1人,选《矩阵变换和坐标系与参数方程》的有5人,第二小组选《数学史与不等式选讲》的有2人,选《矩阵变换和坐标系与参数方程》的有4人,现从第一、第二两小组各任选2人分析得分情况.
(1)求选出的4人均为选《矩阵变换和坐标系与参数方程》的概率;
(2)设X为选出的4个人中选《数学史与不等式选讲》的人数,求X的分布列和数学期望.
(1)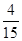 (2) X的分布列为
(2) X的分布列为
1X 0 1 2 3 P 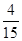
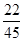

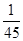
解析解:(1)设“从第一小组选出的2人均选《矩阵变换和坐标系与参数方程》”为事件A,“从第二小组选出的2人均选《矩阵变换和坐标系与参数方程》”为事件B.
由于事件A、B相互独立,
所以P(A)=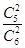 =
=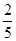 ,P(B)=
,P(B)=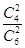 =
=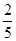 ,
,
所以选出的4人均选《矩阵变换和坐标系与参数方程》的概率为P(A·B)=P(A)·P(B)=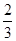 ×
×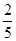 =
=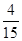 .
.
(2)X可能的取值为0,1,2,3,则
P(X=0)=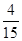 ,P(X=1)=
,P(X=1)=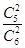 ·
·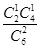 +
+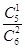 ·
·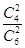 =
=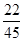 ,
,
P(X=3)=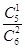 ·
·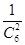 =
=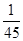 .
.
P(X=2)=1-P(X=0)-P(X=1)-P(X=3)= .
.
故X的分布列为
所以X的数学期望E(X)=0×X 0 1 2 3 P 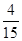
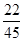

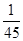
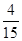 +1×
+1×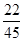 +2×
+2× +3×
+3×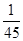 =1 (人).
=1 (人).

2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组,调查 “常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.
(1)能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?
(2)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
 | 0.010 | 0.005 | 0.001 |
 | 6.635 | 7.879 | 10.828 |

经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出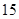 条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
罗非鱼的汞含量(ppm)
 | 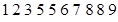 |
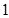 | 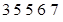 |
《中华人民共和国环境保护法》规定食品的汞含量不得超过
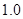 ppm.
ppm.(1)检查人员从这
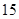 条鱼中,随机抽出
条鱼中,随机抽出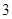 条,求
条,求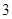 条中恰有
条中恰有 条汞含量超标的概率;
条汞含量超标的概率;(2)若从这批数量很大的鱼中任选
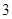 条鱼,记
条鱼,记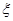 表示抽到的汞含量超标的鱼的条数.以此
表示抽到的汞含量超标的鱼的条数.以此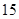 条鱼的样本数据来估计这批数量很大的鱼的总体数据,求
条鱼的样本数据来估计这批数量很大的鱼的总体数据,求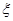 的分布列及数学期望
的分布列及数学期望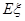 .
.  月
月 日至
日至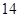 日的空气质量指数趋势图,空气质量指数(
日的空气质量指数趋势图,空气质量指数(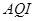 )小于
)小于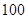 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于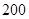 表示空气重度污染,某人随机选择
表示空气重度污染,某人随机选择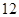 日中的某一天到达该市,并停留
日中的某一天到达该市,并停留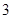 天.
天.
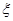 是此人停留期间空气重度污染的天数,求
是此人停留期间空气重度污染的天数,求