题目内容
已知函数 (a ,b
(a ,b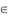 R,e为自然对数的底数),
R,e为自然对数的底数), .
.
(I )当b=2时,若 存在单调递增区间,求a的取值范围;
存在单调递增区间,求a的取值范围;
(II)当a>0 时,设 的图象C1与
的图象C1与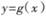 的图象C2相交于两个不同的点P、Q,过线段PQ的中点作x轴的垂线交C1于点
的图象C2相交于两个不同的点P、Q,过线段PQ的中点作x轴的垂线交C1于点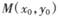 ,求证
,求证 .
.
【答案】
(Ⅰ) .(Ⅱ)见解析
.(Ⅱ)见解析
【解析】(Ⅰ)先求出函数的导数,然后利用条件转化为方程有解问题;(Ⅱ)构造函数,利用导数法研究函数的单调性。
(Ⅰ)当 时,若
时,若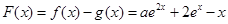 ,则
,则
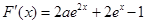 ,原命题等价于
,原命题等价于 在R上有解.…2分
在R上有解.…2分
法一:当 时,显然成立;
时,显然成立;
当 时,
时,
∴  ,即
,即 .综合所述
.综合所述  .…………………5分
.…………………5分
法二:等价于 在R上有解,即∴
在R上有解,即∴  .………………5分
.………………5分
(Ⅱ)设 ,不妨设
,不妨设 ,则
,则 ,
,
 ,
, ,
,
两式相减得: ,……………7分
,……………7分
整理得

则 ,于是
,于是 ,……9分
,……9分
而
令 ,则设
,则设 ,则
,则
 ,
,
∴  在
在 上单调递增,则
上单调递增,则 ,于是有
,于是有 ,即
,即 ,且
,且 ,∴
,∴  ,即
,即 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
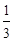 x3+ax2+bx, a , b
x3+ax2+bx, a , b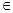 R.
R.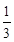 x3+ax2+bx, a
, b
x3+ax2+bx, a
, b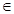 R.
R. x3+ax2+bx, a , b
x3+ax2+bx, a , b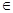 R.
R.