题目内容
已知函数f (x)＝
x3＋ax2＋bx， a , b
R．
(Ⅰ) 曲线C：y＝f (x) 经过点P (1，2)，且曲线C在点P处的切线平行于直线y＝2x＋1，求a，b的值；
(Ⅱ) 已知f (x)在区间 (1，2) 内存在两个极值点，求证：0＜a＋b＜2．
本题主要考查函数的极值概念、导数运算法则、导数应用及二次方程根的分布等基础知识，同时考查抽象概括能力和推理论证能力。满分15分。
(Ⅰ)解:
＝
，
由题设知：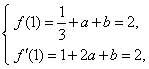
解得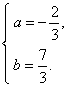
…………6分
(Ⅱ)解：因为
在区间
内存在两个极值点 ，
所以
，即
在内有两个不等的实根．
故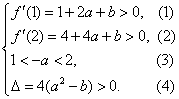
由 (1)+(3)得
.
由（4）得
，
因
，故
，从而
.
所以
． …………15分
练习册系列答案
名校课堂系列答案
相关题目
)x有两个零点x1，x2，则有