题目内容
如图,ABCD是边长为2的正方形,ED⊥平面ABCD, ED="1," EF//BD且2EF=BD.
(1)求证:平面EAC⊥平面BDEF;
(2)求几何体ABCDEF的体积.
(1)要证明平面EAC⊥平面BDEF垂直,关键是证明AC⊥平面BDEF
(2)2
解析试题分析:(1)∵ ED⊥平面ABCD,AC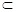 平面ABCD,
平面ABCD,
∴ ED⊥AC.
∵ ABCD是正方形,
∴ BD⊥AC,
∴ AC⊥平面BDEF.
又AC?平面EAC,故平面EAC⊥平面BDEF.
(2)连结FO,∵ EF
 DO,
DO,
∴ 四边形EFOD是平行四边形.
由ED⊥平面ABCD可得ED⊥DO,
∴ 四边形EFOD是矩形.
∵ 平面EAC⊥平面BDEF.
∴ 点F到平面ACE的距离等于就是Rt△EFO斜边EO上的高,
且高h=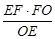 =
=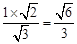 .
.
∴几何体ABCDEF的体积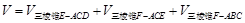
=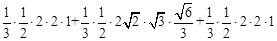
=2.
考点:面面垂直,棱锥的体积
点评:主要是考查了体积公式以及面面垂直的证明,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
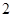 的三棱柱
的三棱柱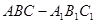 中,侧面
中,侧面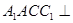 底面
底面 ,
, .
.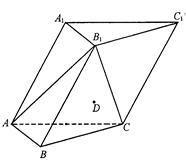
 与平面
与平面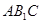 所成角的正弦值的大小;
所成角的正弦值的大小; 满足
满足 ,在直线
,在直线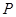 ,使
,使 ?若存在,请确定点
?若存在,请确定点
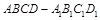 ,中,
,中, ,点
,点 在棱AB上移动.
在棱AB上移动.
 ;
;  的中点时,求点
的中点时,求点 的距离;
的距离;  等于何值时,二面角
等于何值时,二面角 的大小为
的大小为 .
. 的边长为6,
的边长为6, ,
,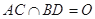 .将菱形
.将菱形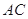 折起,得到三棱锥 ,点
折起,得到三棱锥 ,点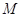 是棱
是棱 的中点,
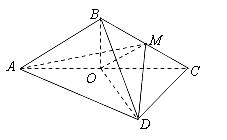
的中点,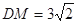 .
.
 ;
; 的体积.
的体积. ,F为CE上的点,且BF
,F为CE上的点,且BF 平面ACE,AC与BD交于点G
平面ACE,AC与BD交于点G


 平面ADE;
平面ADE; ,∠BCC1=60°.
,∠BCC1=60°.