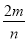题目内容
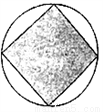
我们知道,可以用模拟的方法估计圆周率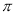 的近似值,如图,在圆内随机撒一把豆子,统计落在其内接正方形中的豆子数目,若豆子总数为
的近似值,如图,在圆内随机撒一把豆子,统计落在其内接正方形中的豆子数目,若豆子总数为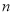 ,落在正方形内的豆子数为
,落在正方形内的豆子数为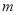 ,则圆周率
,则圆周率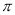 的估算值是
的估算值是
A. 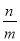 B.
B. 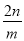 C.
C. 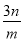 D.
D. 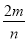
练习册系列答案
相关题目
题目内容
我们知道,可以用模拟的方法估计圆周率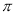 的近似值,如图,在圆内随机撒一把豆子,统计落在其内接正方形中的豆子数目,若豆子总数为
的近似值,如图,在圆内随机撒一把豆子,统计落在其内接正方形中的豆子数目,若豆子总数为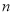 ,落在正方形内的豆子数为
,落在正方形内的豆子数为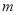 ,则圆周率
,则圆周率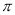 的估算值是
的估算值是

A. 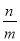 B.
B. 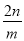 C.
C. 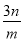 D.
D.