题目内容
已知函数f（x）=2sinωx在区间[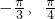
]上的最小值为-2，则ω的取值范围是
- A.
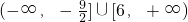
- B.
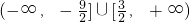
- C.（-∞，-2]∪[6，+∞）
- D.
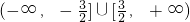
D
分析：先根据x的范围求出ωx的范围，根据函数f（x）在区间[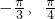]上的最小值为-2，可得到-
ω≤-
，即ω≥
，然后对ω分大于0和小于0两种情况讨论最值可确定答案．
解答：当ω＞0时，-ω≤ωx≤
ω，
由题意知-ω≤-，即ω≥，
当ω＜0时，ω≤ωx≤-ω，
由题意知ω≤-，即ω≤-2，
综上知，ω的取值范围是（-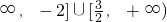
∪[
）．
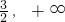故选D．
点评：本题主要考查正弦函数的单调性和最值问题．考查三角函数基础知识的掌握程度，三角函数是高考的一个重要考点一定要强化复习．
分析：先根据x的范围求出ωx的范围，根据函数f（x）在区间[
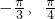]上的最小值为-2，可得到-ω≤-，即ω≥，然后对ω分大于0和小于0两种情况讨论最值可确定答案．解答：当ω＞0时，-
ω≤ωx≤ω，由题意知-
ω≤-，即ω≥，当ω＜0时，
ω≤ωx≤-ω，由题意知
ω≤-，即ω≤-2，综上知，ω的取值范围是（-
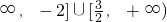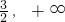∪[）．故选D．
点评：本题主要考查正弦函数的单调性和最值问题．考查三角函数基础知识的掌握程度，三角函数是高考的一个重要考点一定要强化复习．
练习册系列答案
相关题目