题目内容
若椭圆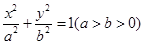 的左、右焦点分别为F1、F2,线段F1F2被抛物线
的左、右焦点分别为F1、F2,线段F1F2被抛物线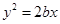 的焦点分成5:3两段,则此椭圆的离心率为
( )
A.
的焦点分成5:3两段,则此椭圆的离心率为
( )
A.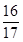 B.
B.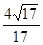 C.
C.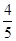 D.
D.
【答案】
D
【解析】解:
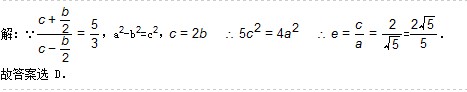

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
题目内容
若椭圆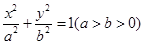 的左、右焦点分别为F1、F2,线段F1F2被抛物线
的左、右焦点分别为F1、F2,线段F1F2被抛物线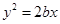 的焦点分成5:3两段,则此椭圆的离心率为
( )
A.
的焦点分成5:3两段,则此椭圆的离心率为
( )
A.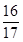 B.
B.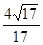 C.
C.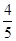 D.
D.
D
【解析】解:
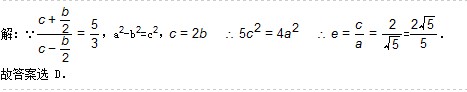

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案