题目内容
下列命题中,真命题的个数为( )
①x2+bx+c=0有一根大于1,另一根小于1的充要条件是1+b+c<0
②当a≥2时,y=
+
的最小值为1
③x2-mx+1≥0对于x>0恒成立,则m≤2
④x≥1的一个充分不必要条件是x=4.
①x2+bx+c=0有一根大于1,另一根小于1的充要条件是1+b+c<0
②当a≥2时,y=
| a |
| 1 | ||
|
③x2-mx+1≥0对于x>0恒成立,则m≤2
④x≥1的一个充分不必要条件是x=4.
分析:①设f(x)=x2+bx+c=0,方程f(x)=0有一根大于1,一根小于1充要条件是f(1)<0,由此得到①正确;
②y=
+
=
+1+
-1≥2
-1=1,当且仅当
=0时,取最小值,由此得到②不正确;
③不等式x2-mx+1≥0对于任意的x∈R均成立,则m≤2;
④x≥1的一个必要不充分条件是x=4.
②y=
| a |
| 1 | ||
|
| a |
| 1 | ||
|
(
|
| a |
③不等式x2-mx+1≥0对于任意的x∈R均成立,则m≤2;
④x≥1的一个必要不充分条件是x=4.
解答:解:①设f(x)=x2+bx+c=0,方程f(x)=0有一根大于1,一根小于1充要条件是
f(1)<0,即b+c<-1,
∴x2+bx+c=0有一根大于1,另一根小于1的充要条件是1+b+c<0,故①正确;
②y=
+
=
+1+
-1≥2
-1=1,
当且仅当
=0时,取最小值,
∴当a≥2时,y=
+
的最小值为1不正确,故②不正确;
③不等式x2-mx+1≥0对于任意的x∈R均成立,
∴由△=m2-4≤0得:-2≤m≤2.
当m<-2时,x2-mx+1≥0对于x>0恒成立,
∴x2-mx+1≥0对于x>0恒成立,则m≤2.故③正确;
④∵由x≥1,不能得到x=4,x=4⇒x>1,
∴x≥1的一个必要不充分条件是x=4,故④不正确.
故选B.
f(1)<0,即b+c<-1,
∴x2+bx+c=0有一根大于1,另一根小于1的充要条件是1+b+c<0,故①正确;
②y=
| a |
| 1 | ||
|
| a |
| 1 | ||
|
(
|
当且仅当
| a |
∴当a≥2时,y=
| a |
| 1 | ||
|
③不等式x2-mx+1≥0对于任意的x∈R均成立,
∴由△=m2-4≤0得:-2≤m≤2.
当m<-2时,x2-mx+1≥0对于x>0恒成立,
∴x2-mx+1≥0对于x>0恒成立,则m≤2.故③正确;
④∵由x≥1,不能得到x=4,x=4⇒x>1,
∴x≥1的一个必要不充分条件是x=4,故④不正确.
故选B.
点评:本题考查命题的真假判断,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 ,则
,则 ”的逆命题
”的逆命题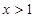 ,则
,则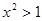 ”的否命题
”的否命题 ,则
,则 ”的否命题
”的否命题 ,则
,则