题目内容
已知直线l与椭圆C: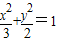 交于P(x1,y1),Q(x2,y2)两不同点,且△OPQ的面积S△OPQ=
交于P(x1,y1),Q(x2,y2)两不同点,且△OPQ的面积S△OPQ=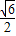 ,其中O为坐标原点.
,其中O为坐标原点.(Ⅰ)证明x12+x22和y12+y22均为定值;
(Ⅱ)设线段PQ的中点为M,求|OM|•|PQ|的最大值;
(Ⅲ)椭圆C上是否存在点D,E,G,使得S△ODE=S△ODG=S△OEG=
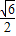 ?若存在,判断△DEG的形状;若不存在,请说明理由.
?若存在,判断△DEG的形状;若不存在,请说明理由.
【答案】分析:(Ⅰ)根据已知设出直线l的方程,利用弦长公式求出|PQ|的长,利用点到直线的距离公式求点O到直线l的距离,根据三角形面积公式,即可求得x12+x22和y12+y22均为定值;
(Ⅱ)由(I)可求线段PQ的中点为M,代入|OM|•|PQ|并利用基本不等式求最值;(Ⅲ)假设存在D(u,v),E(x1,y1),G(x2,y2),使得S△ODE=S△ODG=S△OEG=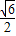
由(Ⅰ)得u2+x12=3,u2+x22=3,x12+x22=3;v2+y12=2,v2+y22=2,y12+y22=2,从而求得点D,E,G,的坐标,可以求出直线DE、DG、EG的方程,从而得到结论.
解答:解:(Ⅰ)1°当直线l的斜率不存在时,P,Q两点关于x轴对称,
所以x1=x2,y1=-y2,
∵P(x1,y1)在椭圆上,
∴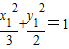 ①
①
又∵S△OPQ=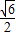 ,
,
∴|x1||y1|=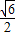 ②
②
由①②得|x1|= ,|y1|=1.此时x12+x22=3,y12+y22=2;
,|y1|=1.此时x12+x22=3,y12+y22=2;
2°当直线l的斜率存在时,是直线l的方程为y=kx+m(m≠0),将其代入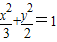 得
得
(3k2+2)x2+6kmx+3(m2-2)=0,△=36k2m2-12(3k2+2)(m2-2)>0
即3k2+2>m2,
又x1+x2=-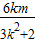 ,x1•x2=
,x1•x2=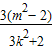 ,
,
∴|PQ|=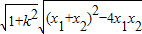 =
=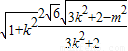 ,
,
∵点O到直线l的距离为d=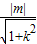 ,
,
∴S△OPQ=
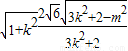
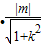 =
=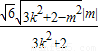 ,
,
又S△OPQ=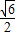 ,
,
整理得3k2+2=2m2,此时x12+x22=(x1+x2)2-2x1x2=(-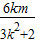 )2-2
)2-2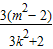 =3,
=3,
y12+y22= (3-x12)+
(3-x12)+ (3-x22)=4-
(3-x22)=4- (x12+x22)=2;
(x12+x22)=2;
综上所述x12+x22=3,y12+y22=2.结论成立.
(Ⅱ)1°当直线l的斜率不存在时,由(Ⅰ)知
|OM|=|x1|=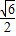 ,|PQ|=2|y1|=2,
,|PQ|=2|y1|=2,
因此|OM|•|PQ|=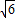 .
.
2°当直线l的斜率存在时,由(Ⅰ)知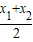 =-
=-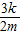 ,
,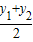 =k
=k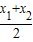 +m=
+m=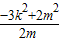 =
=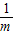
|OM|2=(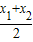 )2+(
)2+(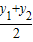 )2=
)2=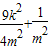 =
= ,
,
|PQ|2=(1+k2)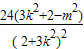 =
=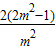 =2(2+
=2(2+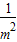 ),
),
所以|OM|2|PQ|2=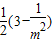 ×
×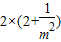 =(3-
=(3-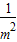 )(2+
)(2+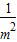 )
)
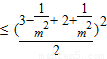 =
=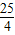 .
.
|OM|•|PQ|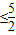 .当且仅当
.当且仅当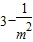 =2+
=2+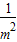 ,
,
即m=±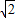 时,等号成立.
时,等号成立.
综合1°2°得|OM|•|PQ|的最大值为 ;
;
(Ⅲ)椭圆C上不存在三点D,E,G,使得S△ODE=S△ODG=S△OEG=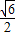 ,
,
证明:假设存在D(u,v),E(x1,y1),G(x2,y2),使得S△ODE=S△ODG=S△OEG=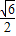
由(Ⅰ)得
u2+x12=3,u2+x22=3,x12+x22=3;v2+y12=2,v2+y22=2,y12+y22=2
解得u2=x12=x22= ;v2=y12=y22=1.
;v2=y12=y22=1.
因此u,x1,x2只能从±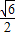 中选取,
中选取,
v,y1,y2只能从±1中选取,
因此点D,E,G,只能在(±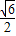 ,±1)这四点中选取三个不同点,
,±1)这四点中选取三个不同点,
而这三点的两两连线中必有一条过原点,与S△ODE=S△ODG=S△OEG=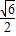 矛盾.
矛盾.
所以椭圆C上不存在满足条件的三点D,E,G.
点评:此题是个难题.本题考查了直线与椭圆的位置关系,弦长公式和点到直线的距离公式,是一道综合性的试题,考查了学生综合运用知识解决问题的能力.其中问题(III)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.
(Ⅱ)由(I)可求线段PQ的中点为M,代入|OM|•|PQ|并利用基本不等式求最值;(Ⅲ)假设存在D(u,v),E(x1,y1),G(x2,y2),使得S△ODE=S△ODG=S△OEG=
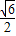
由(Ⅰ)得u2+x12=3,u2+x22=3,x12+x22=3;v2+y12=2,v2+y22=2,y12+y22=2,从而求得点D,E,G,的坐标,可以求出直线DE、DG、EG的方程,从而得到结论.
解答:解:(Ⅰ)1°当直线l的斜率不存在时,P,Q两点关于x轴对称,
所以x1=x2,y1=-y2,
∵P(x1,y1)在椭圆上,
∴
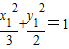 ①
①又∵S△OPQ=
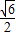 ,
,∴|x1||y1|=
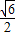 ②
②由①②得|x1|=
 ,|y1|=1.此时x12+x22=3,y12+y22=2;
,|y1|=1.此时x12+x22=3,y12+y22=2;2°当直线l的斜率存在时,是直线l的方程为y=kx+m(m≠0),将其代入
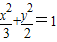 得
得(3k2+2)x2+6kmx+3(m2-2)=0,△=36k2m2-12(3k2+2)(m2-2)>0
即3k2+2>m2,
又x1+x2=-
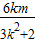 ,x1•x2=
,x1•x2=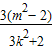 ,
,∴|PQ|=
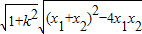 =
=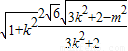 ,
,∵点O到直线l的距离为d=
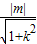 ,
,∴S△OPQ=

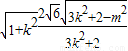
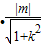 =
=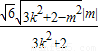 ,
,又S△OPQ=
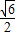 ,
,整理得3k2+2=2m2,此时x12+x22=(x1+x2)2-2x1x2=(-
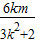 )2-2
)2-2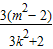 =3,
=3,y12+y22=
 (3-x12)+
(3-x12)+ (3-x22)=4-
(3-x22)=4- (x12+x22)=2;
(x12+x22)=2;综上所述x12+x22=3,y12+y22=2.结论成立.
(Ⅱ)1°当直线l的斜率不存在时,由(Ⅰ)知
|OM|=|x1|=
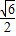 ,|PQ|=2|y1|=2,
,|PQ|=2|y1|=2,因此|OM|•|PQ|=
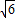 .
.2°当直线l的斜率存在时,由(Ⅰ)知
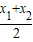 =-
=-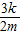 ,
,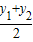 =k
=k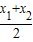 +m=
+m=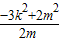 =
=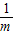
|OM|2=(
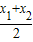 )2+(
)2+(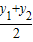 )2=
)2=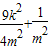 =
= ,
,|PQ|2=(1+k2)
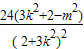 =
=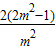 =2(2+
=2(2+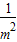 ),
),所以|OM|2|PQ|2=
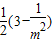 ×
×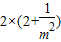 =(3-
=(3-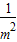 )(2+
)(2+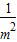 )
)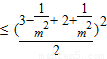 =
=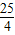 .
.|OM|•|PQ|
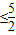 .当且仅当
.当且仅当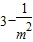 =2+
=2+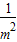 ,
,即m=±
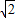 时,等号成立.
时,等号成立.综合1°2°得|OM|•|PQ|的最大值为
 ;
;(Ⅲ)椭圆C上不存在三点D,E,G,使得S△ODE=S△ODG=S△OEG=
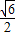 ,
,证明:假设存在D(u,v),E(x1,y1),G(x2,y2),使得S△ODE=S△ODG=S△OEG=
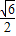
由(Ⅰ)得
u2+x12=3,u2+x22=3,x12+x22=3;v2+y12=2,v2+y22=2,y12+y22=2
解得u2=x12=x22=
 ;v2=y12=y22=1.
;v2=y12=y22=1.因此u,x1,x2只能从±
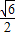 中选取,
中选取,v,y1,y2只能从±1中选取,
因此点D,E,G,只能在(±
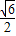 ,±1)这四点中选取三个不同点,
,±1)这四点中选取三个不同点,而这三点的两两连线中必有一条过原点,与S△ODE=S△ODG=S△OEG=
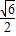 矛盾.
矛盾.所以椭圆C上不存在满足条件的三点D,E,G.
点评:此题是个难题.本题考查了直线与椭圆的位置关系,弦长公式和点到直线的距离公式,是一道综合性的试题,考查了学生综合运用知识解决问题的能力.其中问题(III)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
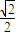 的椭圆C:
的椭圆C: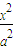 +
+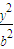 =1(a>b>0)过点M(
=1(a>b>0)过点M(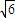 ,1),O为坐标原点.
,1),O为坐标原点. 的一条切线,试证明∠AOB=
的一条切线,试证明∠AOB=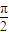 .它的逆命题成立吗?若成立,请给出证明;否则,请说明理由.
.它的逆命题成立吗?若成立,请给出证明;否则,请说明理由.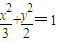 交于P(x1,y1),Q(x2,y2)两不同点,且△OPQ的面积S△OPQ=
交于P(x1,y1),Q(x2,y2)两不同点,且△OPQ的面积S△OPQ=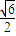 ,其中O为坐标原点.
,其中O为坐标原点.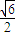 ?若存在,判断△DEG的形状;若不存在,请说明理由.
?若存在,判断△DEG的形状;若不存在,请说明理由.