题目内容
已知函数![]() .
.
(1)函数![]() 在区间(0,+∞)_k是增函数还是增函数?证明你的结论;
在区间(0,+∞)_k是增函数还是增函数?证明你的结论;
(2)当![]() >0时,
>0时,![]() >
>![]() 恒成立,求正整数
恒成立,求正整数![]() 的最大值.
的最大值.
解:(1) ![]()
=![]()
∵![]() >0,∴
>0,∴![]() 2>0,
2>0,![]() >o,ln(
>o,ln(![]() +1)>0,
+1)>0,
∴![]() <0.
<0.
因此函数![]() 在区间(0,+∞)上是减函数.
在区间(0,+∞)上是减函数.
(2)当![]() >0时,
>0时,![]() >
>![]() 恒成立,
恒成立,
令![]() =1,有
=1,有![]() <2(1+ln2).
<2(1+ln2).
又![]() 为正整数,∴
为正整数,∴![]() 的最大值不大于3.
的最大值不大于3.
下面证明当![]() =3时,
=3时,![]() >
>![]() (
(![]() >0)恒成立,
>0)恒成立,
即证当![]() >0时,(
>0时,(![]() +1)ln(
+1)ln(![]() +1)+1―2
+1)+1―2![]() >0恒成立
>0恒成立
令g(![]() )=(
)=(![]() +1)ln(
+1)ln(![]() +1)+1―2
+1)+1―2![]() ,
,
则g’(![]() )=ln(
)=ln(![]() +1)―1,
+1)―1,
当![]() >e一1时,g’(
>e一1时,g’(![]() )>0;当0<
)>0;当0<![]() <e一1时,g’(
<e一1时,g’(![]() )<0,
)<0,
∴当![]() =e一1时,g(
=e一1时,g(![]() )取得最小值g(e-1)=3一e>0.
)取得最小值g(e-1)=3一e>0.
当![]() >0时,(
>0时,(![]() +1)ln(
+1)ln(![]() +1)+1―2
+1)+1―2![]() >0恒成立.
>0恒成立.
因此正整数![]() 的最大值为3.
的最大值为3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
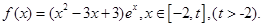
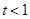 时,求函数
时,求函数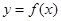 的单调区间;
的单调区间;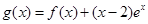 ,试问函数
,试问函数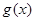 在
在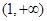 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
 的定义域;
的定义域; 为何值时,函数值大于1.
为何值时,函数值大于1.
 ,
, ,
, ,
, 这几个函数值,你能发现f(x)与
这几个函数值,你能发现f(x)与 有什么关系?并证明你的结论;
有什么关系?并证明你的结论;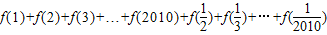 的值;
的值; 在区间(0,+∞)上的单调性.
在区间(0,+∞)上的单调性.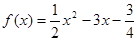
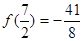 ,求
,求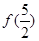
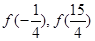 的大小
的大小