题目内容
19.设△ABC的内角A,B,C所对的边长分别为a,b,c,且$\frac{cosC}{cosA}$=$\frac{2b-\sqrt{3}c}{\sqrt{3}a}$.(1)求角A的大小;
(2)设点M为BC的中点,若角B=$\frac{π}{6}$,且AM=$\sqrt{7}$,求△ABC的面积.
分析 (1)由$\frac{cosC}{cosA}$=$\frac{2b-\sqrt{3}c}{\sqrt{3}a}$,利用正弦定理可得:$\frac{cosC}{cosA}=\frac{2sinB-\sqrt{3}sinC}{\sqrt{3}sinA}$,化简利用两角和差的正弦公式、三角形内角和定理、诱导公式即可得出.
(2)设BC=a,则AC=a,取AB的中点D,连接CD.则BD=$\frac{\sqrt{3}}{2}$a,可得AB=$\sqrt{3}$a.在△ABM中,由余弦定理可得AM2=BM2+AB2-2BM•ABcosB,解出a,再利用三角形面积计算公式即可得出.
解答 解:(1)∵$\frac{cosC}{cosA}$=$\frac{2b-\sqrt{3}c}{\sqrt{3}a}$,如图所示,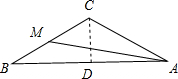
由正弦定理可得:$\frac{cosC}{cosA}=\frac{2sinB-\sqrt{3}sinC}{\sqrt{3}sinA}$,
化为$\sqrt{3}$(sinAcosC+cosAsinC)=2sinBcosA,
∴$\sqrt{3}sin(A+C)$=2sinBcosA,
∴$\sqrt{3}$sinB=2sinBcosA,
∵sinB≠0,
∴cosA=$\frac{\sqrt{3}}{2}$,
∵A∈(0,π),∴$A=\frac{π}{6}$.
(2)设BC=a,则AC=a,取AB的中点D,连接CD.
则BD=$\frac{\sqrt{3}}{2}$a,∴AB=$\sqrt{3}$a.
在△ABM中,AM2=BM2+AB2-2BM•ABcosB,
∴7=$\frac{1}{4}{a}^{2}$+3a2-2×$\frac{1}{2}a×\sqrt{3}a×cos\frac{π}{6}$,
化为${a}^{2}=\frac{14}{5}$,解得a=$\frac{\sqrt{70}}{5}$.
∴S△ABC=$\frac{1}{2}{a}^{2}sin\frac{2π}{3}$=$\frac{1}{2}×\frac{14}{5}×\frac{\sqrt{3}}{2}$=$\frac{7\sqrt{3}}{10}$.
点评 本题考查了正弦定理余弦定理、两角和差的正弦公式、三角形内角和定理、诱导公式、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案| 评估得分 | [60,70) | [70,80) | [80,90) | [90,100] |
| 评定等级 | D | C | B | A |
| 频率 | m | 0.62 | 0.32 | 2m |
(Ⅱ)从评定等级为D和A的学校中,任意抽取2所,求抽取的两所学校等级相同的概率.
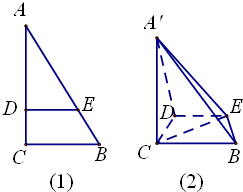 如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2.将△ADE沿DE折起到△A′DE的位置,使A′C⊥CD,如图(2).
如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2.将△ADE沿DE折起到△A′DE的位置,使A′C⊥CD,如图(2).