题目内容
10.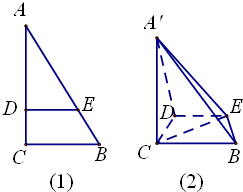 如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2.将△ADE沿DE折起到△A′DE的位置,使A′C⊥CD,如图(2).
如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2.将△ADE沿DE折起到△A′DE的位置,使A′C⊥CD,如图(2).(Ⅰ)求证:DE∥平面A′BC;
(Ⅱ)求证:A′C⊥BE;
(Ⅲ)线段A′D上是否存在点F,使平面CFE⊥平面A′DE.若存在,求出DF的长;若不存在,请说明理由.
分析 (Ⅰ)利用D,E分别为AC,AB上的点,且DE∥BC,结合线面平行的判定证明DE∥平面A′BC;
(Ⅱ)证明A'C⊥平面BCDE,再证明:A′C⊥BE;
(Ⅲ)线段A'D上存在点F,DF=1,使平面CFE⊥平面A′DE.
解答 (I)证明:因为D,E分别为AC,AB上的点,且DE∥BC,
又因为DE?平面A′BC,
所以DE∥平面A′BC…(3分)
(II)证明:因为∠C=90°,DE∥BC,
所以DE⊥CD,DE⊥AD,
由题意可知,DE⊥A′D,…(4分)
又A′D∩CD=D,
所以DE⊥平面A′CD,…(5分)
所以BC⊥平面A′CD,…(6分)
所以BC⊥A′C,…(7分)
又A′C⊥CD,且CD∩BC=C,
所以A′C⊥平面BCDE,…(8分)
又BE?平面BCDE,
所以A′C⊥BE…(9分)
(III)解:线段A′D上存在点F,使平面CFE⊥平面A′DE.
理由如下: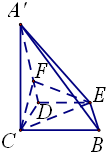
因为A′C⊥CD,
所以,在Rt△A′CD中,过点C作CF⊥A′D于F,
由(II)可知,DE⊥平面A′CD,又CF?平面A′CD
所以DE⊥CF,
又A′D∩DE=D,
所以CF⊥平面A′DE,…(12分)
因为CF?平面CEF,
所以平面CFE⊥平面A′DE,
故线段A′D上存在点F,使平面CFE⊥平面A′DE…(13分)
如图(1),因为DE∥BC,
所以,$\frac{DE}{BC}=\frac{AD}{AC}$,即$\frac{2}{3}=\frac{AD}{6}$,
所以,AD=4,CD=2.
所以,如图(2),在Rt△A′CD中,A′D=4,CD=2
所以,∠A′DC=60°,
在Rt△CFD中,DF=1…(14分)
点评 本题考查线面平行的判定与性质,考查学生分析解决问题的能力,考查探索性问题,有难度.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目