题目内容
已知函数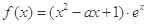 .
.
(I)当a=3时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(II)对任意b>0,f(x)在区间[b-lnb,+∞)上是增函数,求实数a的取值范围.
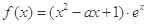 .
.(I)当a=3时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(II)对任意b>0,f(x)在区间[b-lnb,+∞)上是增函数,求实数a的取值范围.
(I)  (II)
(II)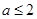
 (II)
(II)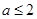
试题分析:(I)
 时,
时,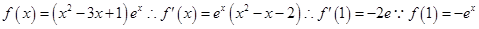
所以切线为

(II)
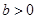 时,设
时,设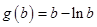

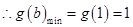
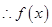 在
在 上是增函数,
上是增函数,
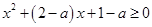 恒成立
恒成立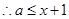 恒成立,
恒成立,
点评:利用导数的几何意义(函数在某一点处的导数值等于该点处的切线斜率)通过导数可求出直线斜率;第二问将单调性转化为导数值的正负,进而将不等式恒成立转化为求函数最值,这种不等式与函数的转化是常考的思路

练习册系列答案
相关题目

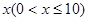 分钟应付话费y元,写出函数解析式并画出函数图象.
分钟应付话费y元,写出函数解析式并画出函数图象.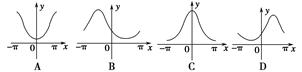
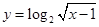 的图像,可将函数
的图像,可将函数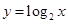 的图像上所有的点的( )
的图像上所有的点的( ) ,横坐标不变,再向右平移1个单位
,横坐标不变,再向右平移1个单位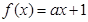 在R上递减,则函数
在R上递减,则函数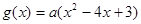 的增区间是 ( )
的增区间是 ( )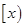 表示大于
表示大于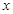 的最小整数,例如
的最小整数,例如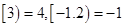 .下列命题
.下列命题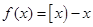 的值域是
的值域是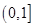 ;②若
;②若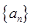 是等差数列,则
是等差数列,则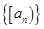 也是等差数列;
也是等差数列;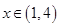 ,则方程
,则方程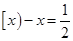 有3个根.
有3个根.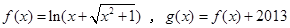 ,下列命题:
,下列命题: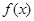 的定义域为
的定义域为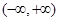 ;
; 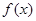 在
在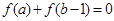 ,则
,则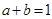 ;
;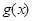 在
在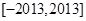 的最大值为M,最小值为m,则M+m=2013
的最大值为M,最小值为m,则M+m=2013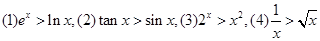 ,则在
,则在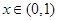 内上述不等式恒成立的个数为( )
内上述不等式恒成立的个数为( )