题目内容
设a,b,m为正整数,若a和b除以m的余数相同,则称a和b对m同余. 记作a=b(modm),已知a=
32+
34+…+
34018,b=a(mod10),则b的值可以是( )
| C | 1 2009 |
| C | 2 2009 |
| C | 2009 2009 |
分析:观察题中式子:a=C2010132+C2010234+…+C2010201034020,先由二项式定理得:1+C2010132+C2010234+…+C2010201034020=(1+9)2010,得到C2010132+C2010234+…+C2010201034020=(1+9)2010-1,即C2010132+C2010234+…+C20102010340209(mod10),而2009≡9(mod10),从而得出b的值.
解答:解:由二项式定理得:∵1+C2010132+C2010234+…+C2010201034020=(1+9)2010,
∴C2010132+C2010234+…+C2010201034020=(1+9)2010-1,
即C2010132+C2010234+…+C2010201034020除以10的余数为:9.
而2009≡9(mod10),则b的值可以是2009,
故选B.
∴C2010132+C2010234+…+C2010201034020=(1+9)2010-1,
即C2010132+C2010234+…+C2010201034020除以10的余数为:9.
而2009≡9(mod10),则b的值可以是2009,
故选B.
点评:本题主要考查二项式定理的应用,这是一道新运算类的题目,其特点一般是“新”而不“难”,处理的方法一般为:根据新运算的定义,将已知中的数据代入进行运算,易得最终结果,属于中档题.

练习册系列答案
相关题目
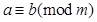 ,已知
,已知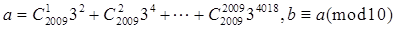 ,则b的值可以是 ( )
,则b的值可以是 ( )