题目内容
设a,b,m为正整数,若a和b除以m的余数相同,则称a和b对m同余.记作a≡b(bmodm),已知a=C2010132+C2010234+…+C2010201034020,b≡a(mod10),则b的值可以是( )
| A.2007 | B.2008 | C.2009 | D.2010 |
由二项式定理得:
∵1+C2010132+C2010234+…+C2010201034020=(1+9)2010,
∴C2010132+C2010234+…+C2010201034020=(1+9)2010-1,
即C2010132+C2010234+…+C2010201034020除以10的余数为:9.
而2009≡9(mod10),
则b的值可以是2009.
故选C.
∵1+C2010132+C2010234+…+C2010201034020=(1+9)2010,
∴C2010132+C2010234+…+C2010201034020=(1+9)2010-1,
即C2010132+C2010234+…+C2010201034020除以10的余数为:9.
而2009≡9(mod10),
则b的值可以是2009.
故选C.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
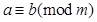 ,已知
,已知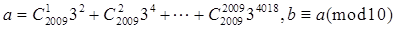 ,则b的值可以是 ( )
,则b的值可以是 ( )