题目内容
(1)在极坐标系中,点P的极坐标为(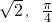 ),点Q是曲线C上的动点,曲线C的极坐标方程为ρ(cosθ-sinθ)+1=0,则P、Q两点之间的距离的最小值为________.
),点Q是曲线C上的动点,曲线C的极坐标方程为ρ(cosθ-sinθ)+1=0,则P、Q两点之间的距离的最小值为________.
(2)已知PA是圆O的切线,切点为A,PA=2,AC是圆O的直径,PC与圆O交于点B,PB=l,则圆D的半径R=________.
解:(1)在极坐标系中,∵点P的极坐标为(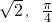 ),故它的直角坐标为(1,1). AC2
),故它的直角坐标为(1,1). AC2
曲线C的极坐标方程为ρ(cosθ-sinθ)+1=0,故它的直角坐标方程为 x-y+1=0,表示一条直线.
则P、Q两点之间的距离的最小值为点P到直线的距离: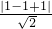 =
= ,故答案为
,故答案为  .
.
(2)由题意可得,△PAC为直角三角形,∴PC= =
=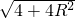 .
.
再由圆的切割线定理可得 PA2=PB•PC,即 4=1×PC,解得 PC=4.
即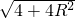 =4,解得 R=
=4,解得 R= ,
,
故答案为 .
.
分析:(1)先求出点P的直角坐标,再求出直线的直角坐标方程,由题意可得P、Q两点之间的距离的最小值为点P到直线的距离,利用点到直线的距离公式求得结果.
(2)由题意可得,△PAC为直角三角形,用勾股定理求出PC,再由圆的切割线定理可得 PA2=PB•PC,由此求出PC的值,由此求得圆D的半径R.
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,圆的切割线定理的应用,属于基础题.
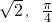 ),故它的直角坐标为(1,1). AC2
),故它的直角坐标为(1,1). AC2曲线C的极坐标方程为ρ(cosθ-sinθ)+1=0,故它的直角坐标方程为 x-y+1=0,表示一条直线.
则P、Q两点之间的距离的最小值为点P到直线的距离:
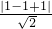 =
= ,故答案为
,故答案为  .
.(2)由题意可得,△PAC为直角三角形,∴PC=
 =
=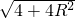 .
.再由圆的切割线定理可得 PA2=PB•PC,即 4=1×PC,解得 PC=4.
即
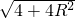 =4,解得 R=
=4,解得 R= ,
,故答案为
 .
.分析:(1)先求出点P的直角坐标,再求出直线的直角坐标方程,由题意可得P、Q两点之间的距离的最小值为点P到直线的距离,利用点到直线的距离公式求得结果.
(2)由题意可得,△PAC为直角三角形,用勾股定理求出PC,再由圆的切割线定理可得 PA2=PB•PC,由此求出PC的值,由此求得圆D的半径R.
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,圆的切割线定理的应用,属于基础题.

练习册系列答案
相关题目