题目内容
下面四个命题:
①已知函数f(x)=
且f(a)+f(4)=4,那么a=-4;
②一组数据18,21,19,a,22的平均数是20,那么这组数据的方差是2;
③已知奇函数f(x)在(0,+∞)为增函数,且f(-1)=0,则不等式f(x)<0的解集{x|x<-1};
④在极坐标系中,圆ρ=-4cosθ的圆心的直角坐标是(-2,0).
其中正确的是
①已知函数f(x)=
|
②一组数据18,21,19,a,22的平均数是20,那么这组数据的方差是2;
③已知奇函数f(x)在(0,+∞)为增函数,且f(-1)=0,则不等式f(x)<0的解集{x|x<-1};
④在极坐标系中,圆ρ=-4cosθ的圆心的直角坐标是(-2,0).
其中正确的是
②,④
②,④
.分析:①注意分段函数在不同区间内的解析式不同,因此要讨论.②利用平均数公式先求出a,进而再利用方差的公式计算即可.
③根据题意画出图象即可求解.④利用极坐标与普通方程的互化公式即可求出.
③根据题意画出图象即可求解.④利用极坐标与普通方程的互化公式即可求出.
解答:解:①∵f(a)+f(4)=4,f(2)=
=2,∴f(a)=2.当a≥0时,则f(a)=
,∴
=2,∴a=4;
当a<0时,f(a)=
,∴
=2,∴a=-4.综上可知,a=±4.故①不正确.
②∵数据18,21,19,a,22的平均数是20,∴(18+21+19+a+22)÷5=20,解得a=20.
∴方差s2=
×[(-2)2+12+(-1)2+02+22]=2,故②正确.
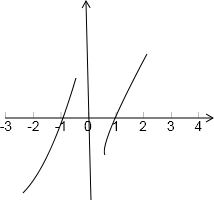
③如图所示,∵函数f(x)是奇函数,∴其图象关于原点对称.∵f(-1)=0,∴f(1)=-f(-1)=0,f(0)=0,∴不等式f(x)<0的解集为{x|x<-1,或0<x<1}.故③不正确.
④由圆ρ=-4cosθ,∴ρ2=-4ρcosθ,即x2+y2+4x=0,∴(x+2)2+y2=4,∴圆ρ=-4cosθ的圆心的直角坐标是(-2,0).
| 4 |
| a |
| a |
当a<0时,f(a)=
| -a |
| -a |
②∵数据18,21,19,a,22的平均数是20,∴(18+21+19+a+22)÷5=20,解得a=20.
∴方差s2=
| 1 |
| 5 |
③如图所示,∵函数f(x)是奇函数,∴其图象关于原点对称.∵f(-1)=0,∴f(1)=-f(-1)=0,f(0)=0,∴不等式f(x)<0的解集为{x|x<-1,或0<x<1}.故③不正确.
④由圆ρ=-4cosθ,∴ρ2=-4ρcosθ,即x2+y2+4x=0,∴(x+2)2+y2=4,∴圆ρ=-4cosθ的圆心的直角坐标是(-2,0).

点评:本题综合考查了函数的性质、不等式、平均数与方差等内容,深刻理解以上内容是解决问题的关键.①

练习册系列答案
相关题目
 ,
, ,
,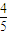 ,
, ,…的通项公式是an=
,…的通项公式是an=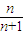 ;
;