题目内容
已知 在
在 时有极大值6,在
时有极大值6,在 时有极小值
时有极小值
求 的值;并求
的值;并求 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值.
 在
在 时有极大值6,在
时有极大值6,在 时有极小值
时有极小值求
 的值;并求
的值;并求 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值.在区间[-3,3]上,当 时,
时,
 时,
时,
 时,
时,
 时,
时,
试题分析:解:
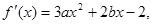 2分
2分由条件知
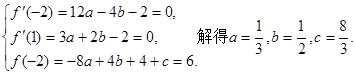 6分
6分
| x | -3 | (-3,-2) | -2 | (-2,1) | 1 | (1,3) | 3 |
 | | + | 0 | - | 0 | + | |
 |  | ↗ | 6 | ↘ |  | ↗ |  |
由上表知,在区间[-3,3]上,当
 时,
时,
 时,
时, 12分
12分点评:解决的关键是根据导数的符号判定函数单调性,进而得到极值和最值,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, .
. 为
为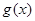 的导函数,若不等式
的导函数,若不等式 在
在 上有解,求实数
上有解,求实数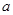 的取值范围;
的取值范围; ,对任意的
,对任意的 ,不等式
,不等式 恒成立,求m(m∈Z,m
恒成立,求m(m∈Z,m 1)的值.
1)的值.
 的单调区间;
的单调区间;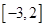 上的最值
上的最值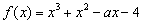 在区间
在区间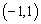 恰有一个极值点,则实数
恰有一个极值点,则实数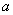 的取值范围为 。
的取值范围为 。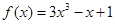 。
。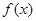 的单调递减区间;
的单调递减区间;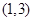 的切线方程;
的切线方程;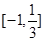 上的最大值与最小值。
上的最大值与最小值。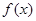 的定义域为
的定义域为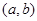 ,其导函数
,其导函数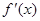 在
在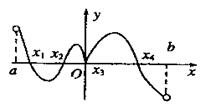
 是
是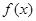 的导函数,
的导函数,
 在
在 处取得极值.
处取得极值. 与
与 满足的关系式;
满足的关系式; ,求函数
,求函数 的单调区间;
的单调区间; ,若存在
,若存在 ,
, ,使得
,使得
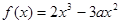 ,
,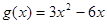 ,又函数
,又函数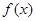 在
在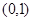 单调递减,而在
单调递减,而在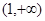 单调递增.
单调递增.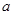 的值;
的值;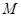 的最小值,使对
的最小值,使对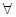
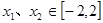 ,有
,有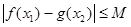 成立;
成立;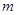 ,使得
,使得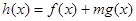 在
在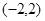 上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.