题目内容
16．已知曲线y=x2（1）判断曲线在点P（1，1）处是否有切线，如果有，求切线的斜率，然后写出切线的方程；
（2）求曲线y=f（x）在x=2处的切线斜率．
分析 （1）求出函数的导数，令x=1求得切线的斜率，由点斜式方程即可得到切线的方程；
（2）求出函数的导数，令x=2即可得到切线的斜率．
解答 解：（1）y=x2的导数为y′=2x，
即有曲线在点P（1，1）处有切线．
即有曲线在点P（1，1）处的切线的斜率为k=2，
则曲线在点P（1，1）处的切线方程为y-1=2（x-1），
即为2x-y-1=0；
（2）由y=x2的导数为y′=2x，
则有曲线y=f（x）在x=2处的切线斜率为2×2=4．
点评 本题考查导数的运用：求切线的方程，掌握导数的几何意义：函数在某点处的导数即为曲线在该点处的切线的斜率，同时考查直线的点斜式方程，属于基础题．
练习册系列答案
相关题目
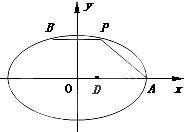如图，在平面直角坐标系xOy中，已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点，点D（1，0），点P，B在椭圆上，$\overrightarrow{BP}$=$\overrightarrow{DA}$．
如图，在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体，已知BB1⊥平面BCD，四边形ABCD是平行四边形，∠ABC=120°，AB=4，AD=2，BB1=1，设O是线段BD的中点．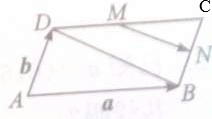
如图，?ABCD中，M、N分别是边DC、BC的中点．
5．对?a，b∈R，记min{a，b}=$\left\{\begin{array}{l}{a，（a＜b）}\\{b（a≥b）}\end{array}\right.$，则函数f（x）=min{|x+1|，|x-1|}（x∈R）的单调增区间为（ ）
| A． | [0，+∞） | B． | （-∞，0] | C． | （-∞，-1]和[0，1] | D． | [-1，0]和[1，+∞） |