题目内容
1.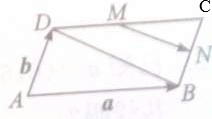 如图,?ABCD中,M、N分别是边DC、BC的中点.
如图,?ABCD中,M、N分别是边DC、BC的中点.(1)求证:MN∥$\frac{1}{2}$DB,MN=$\frac{1}{2}$DB;
(2)设$\overrightarrow{AB}$=a,$\overrightarrow{AD}$=b,且$\overrightarrow{MN}$=$x\overrightarrow{a}+y\overrightarrow{b}$,求x,y的值.
分析 (1)根据题意,在△BCD中,MN为中位线,即得结果;
(2)$x\overrightarrow{a}+y\overrightarrow{b}$=$\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}$=$\frac{1}{2}\overrightarrow{a}-\frac{1}{2}\overrightarrow{b}$,即得结果.
解答 (1)证明:根据题意,在△BCD中,
MN为中位线,所以MN∥$\frac{1}{2}$DB,MN=$\frac{1}{2}$DB;
(2)解:根据题意,可得
$\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}$
=$\frac{1}{2}\overrightarrow{DC}+\frac{1}{2}\overrightarrow{CB}$
=$\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{DA}$
=$\frac{1}{2}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AD}$
=$\frac{1}{2}\overrightarrow{a}-\frac{1}{2}\overrightarrow{b}$,
又$\overrightarrow{MN}=x\overrightarrow{a}+y\overrightarrow{b}$,
所以$x=\frac{1}{2}$,$y=-\frac{1}{2}$.
点评 本题考查向量的运算,将$\overrightarrow{MN}$表示成$\frac{1}{2}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AD}$是解决本题的关键,属基础题.

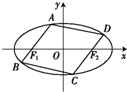 已知椭圆C:$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1的内接平行四边形的一组对边分别经过其两个焦点(如图),则这个平行四边形面积的最大值为( )
已知椭圆C:$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1的内接平行四边形的一组对边分别经过其两个焦点(如图),则这个平行四边形面积的最大值为( )| A. | 8 | B. | 8$\sqrt{3}$ | C. | 16 | D. | 16$\sqrt{3}$ |
| A. | $\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |