题目内容
5.对?a,b∈R,记min{a,b}=$\left\{\begin{array}{l}{a,(a<b)}\\{b(a≥b)}\end{array}\right.$,则函数f(x)=min{|x+1|,|x-1|}(x∈R)的单调增区间为( )| A. | [0,+∞) | B. | (-∞,0] | C. | (-∞,-1]和[0,1] | D. | [-1,0]和[1,+∞) |
分析 运用定义min{a,b},运用分段函数写出f(x)的解析式,再分别讨论各段的单调性,即可得到所求增区间.
解答 解:min{a,b}=$\left\{\begin{array}{l}{a,(a<b)}\\{b(a≥b)}\end{array}\right.$,可得
函数f(x)=min{|x+1|,|x-1|}
当|x-1|<|x+1|,解得x>0,
当|x-1|≥|x+1|,解得x≤0.
则f(x)=$\left\{\begin{array}{l}{|x-1|,x>0}\\{|x+1|,x≤0}\end{array}\right.$,
当x>0时,f(x)=|x-1|在[1,+∞)为递增函数;
当x≤0时,f(x)=|x+1|在[-1,0]为递增函数.
即有f(x)的增区间为[-1,0]和[1,+∞).
故选D.
点评 本题考查函数的单调性,主要考查分段函数的单调区间的求法,理解新定义和运用新定义是解题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
12.已知cos($\frac{π}{6}$+$\frac{α}{2}$)=$\frac{1}{3}$,则sin(α-$\frac{π}{6}$)=( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |
13.底面边长为1的正四棱柱ABCD-A1B1C1D1中,M是DD1的中点,AM与CB1所成角的余弦值为$\frac{\sqrt{10}}{10}$,则点D到平面AMC的距离( )
| A. | $\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
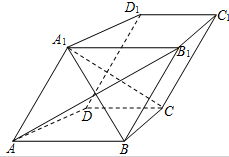 如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB1⊥BC,且AA1=AB.
如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB1⊥BC,且AA1=AB.