题目内容
19.设x1,x2∈R,函数f(x)满足ex=$\frac{1+f(x)}{1-f(x)}$,若f(x1)+f(x2)=1,则f(x1+x2)最小值是$\frac{4}{5}$.分析 由条件求得f(x)的解析式,再由f(x1)+f(x2)=1,可得${e}^{{x}_{1}+{x}_{2}}$=${e}^{{x}_{1}}$+${e}^{{x}_{2}}$+3,运用基本不等式可得${e}^{{x}_{1}+{x}_{2}}$≥9,再由函数的单调性,即可得到最小值.
解答 解:由ex=$\frac{1+f(x)}{1-f(x)}$,可得
f(x)=$\frac{{e}^{x}-1}{{e}^{x}+1}$=1-$\frac{2}{{e}^{x}+1}$,
由f(x1)+f(x2)=1,可得$\frac{1}{1+{e}^{{x}_{1}}}$+$\frac{1}{1+{e}^{{x}_{2}}}$=$\frac{1}{2}$,
即为${e}^{{x}_{1}+{x}_{2}}$=${e}^{{x}_{1}}$+${e}^{{x}_{2}}$+3,由${e}^{{x}_{1}}$+${e}^{{x}_{2}}$≥2$\sqrt{{e}^{{x}_{1}+{x}_{2}}}$,
即有${e}^{{x}_{1}+{x}_{2}}$≥2$\sqrt{{e}^{{x}_{1}+{x}_{2}}}$+3,
解得$\sqrt{{e}^{{x}_{1}+{x}_{2}}}$≥3,
即为${e}^{{x}_{1}+{x}_{2}}$≥9,当且仅当x1=x2,取得等号,
则f(x1+x2)=1-$\frac{2}{{e}^{{x}_{1}+{x}_{2}}+1}$≥1-$\frac{2}{9+1}$=$\frac{4}{5}$.
即有最小值为$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 本题考查函数的性质和运用,主要考查指数函数的单调性及运用,同时考查基本不等式的运用:求最值,属于中档题.

| A. | {x|0≤x<2} | B. | {x|-2<x≤-1} | C. | {x|-2<x≤0} | D. | {x|-1≤x≤0} |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
| A. | $\root{3}{2^4}$ | B. | $\root{4}{3^2}$ | C. | $\root{4}{2^3}$ | D. | $\root{2}{4^3}$ |
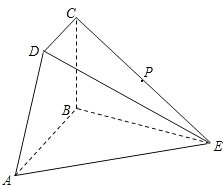 如图所示,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,△ABE为等边三角形,且平面ABCD⊥平面ABE,AB=2CD=2BC=2,P为CE中点.
如图所示,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,△ABE为等边三角形,且平面ABCD⊥平面ABE,AB=2CD=2BC=2,P为CE中点.