题目内容
（本小题满分12分）
已知函数f（x）=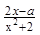
（x∈R）．
⑴当f（1）=1时，求函数f（x）的单调区间；[来源:Zxxk.Com]
⑵设关于x的方程f（x）=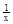
的两个实根为x1,x2 ，且-1≤a≤1,求｜x1-x2｜的最大值；
⑶在（2）的条件下，若对于［-1，1］上的任意实数t，不等式m2+tm+1≥｜x1-x2｜恒成立，求实数m的取值范围．
（1）f（x）的减区间是（-∞，-2］和［1，+∞），增区间是［-2，1］；（2）3；（3）m≥2或m≤-2
【解析】⑴ 由f（1）=1得a=-1 ，……………………………………………………2分[来源:学+科+网]
f′（x）=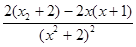
=
=
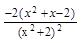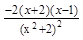≥0……………………4分
-2≤x≤1，所以f（x）的减区间是（-∞，-2］和［1，+∞），增区间是［-2，1］…5分
⑵方程f（x）=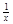
可化为x2-ax-2=0，Δ=a2+8 >0
∴x2-ax-2=0有两不同的实根x1，x2，
则x1+x2=a,x1x2=-2…………………………7分
∴ ｜x1-x2｜=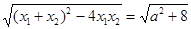
∵-1≤a≤1 ，∴当a=±1时，
∴｜x1-x2｜max=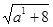
=3…………………………8分
⑶若不等式m2+tm+1≥｜x1-x2｜恒成立，
由⑵可得m2+tm+1≥3，对t∈［-1，1］ 都成立m2+tm-2≥0 ，t∈［-1，1］，
设g（t）=m2+tm-2…………………………………………9分
若使t ∈［-1，1］时g（t）≥0都成立，
则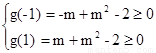
…………11分
解得：m≥2或m≤-2 ，所以m的取值范围是m≥2或m≤-2……………………12分
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
