题目内容
对于n个向量,
,
,…,
,若存在n个不全为零的实数k1,k2,…kn,使得k1
1+k2
2+…+kn
n=0成立,则称向量
,
,…,
,是线性相关的.按此规定,能使向量
=(1,0),
=(1,-1),
=(2,2)是线性相关的实数k1,k2,k3的值依次为______.(只需写出一组值即可)
| a1 |
| a2 |
| an |
| a |
| a |
| a |
| a1 |
| a2 |
| an |
| a1 |
| a2 |
| a3 |
设存在不全为零的实数k1,k2,k3使得k1
+k2
+k3
=
,则
,
不妨令k2=2,则k3=1,k1=-4.
∴能使向量
=(1,0),
=(1,-1),
=(2,2)是线性相关的实数k1,k2,k3的值依次可以为-4,2,1.
故答案为-4,2,1.
| a1 |
| a2 |
| a3 |
| 0 |
|
不妨令k2=2,则k3=1,k1=-4.
∴能使向量
| a1 |
| a2 |
| a3 |
故答案为-4,2,1.

练习册系列答案
相关题目
 是
是 的三条高,求证:
的三条高,求证:
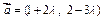 与
与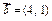 共线,则
共线,则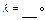
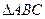 和点M满足
和点M满足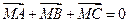 .若存在实
.若存在实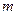 使得
使得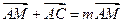 成立,则
成立,则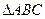 的内角,
的内角,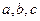 分别是其对边长,向量
分别是其对边长,向量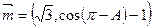 ,
,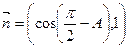 ,
,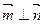 .求角A的大小;
.求角A的大小;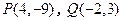 ,则直线
,则直线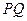 与
与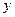 轴的交点分有向线段
轴的交点分有向线段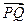 的比为 。
的比为 。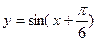 的图象按向量
的图象按向量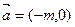 平移所得的图象关于
平移所得的图象关于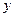 轴对称,则
轴对称,则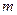 最小正值是 ( )
最小正值是 ( )


