题目内容

P为直径AB=4的半圆上一点，C为AB延长线上一点，BC=2，△PCQ为正△，问∠POC为多大时，四边形OCQP面积最大，最大面积为多少？
分析：设∠POC=α，在△OPC中由余弦定理求得PC，进而表示出S△PCQ，利用两角和公式化简整理，根据正弦函数的性质求得最大值．
解答：解：设∠POC=α，在△OPC中由余弦定理得PC2=20-16cosα
S△OPC=4sinα，S△PCQ=5
3
-4
3
cosαSOCPQ=4sinα-4
3
cosα+5
3
=8sin(α-
π
3
)+5
3

故当α=
5
6
π时，四边形OCQP面积最大，最大面积为8+5
3
点评：本题主要考查了余弦定理的应用．考查了学生对基础知识的理解和运用．
练习册系列答案
相关题目
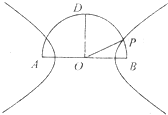如图，在以点O为圆心，AB为直径的半圆中，D为半圆弧的中心，P为半圆弧上一点，且AB=4，∠POB=30°，双曲线C以A，B为焦点且经过点P．
（1）建立适当的平面直角坐标系，求双曲线C的方程；
（2）设过点D的直线l与双曲线C相交于不同两点E、F，若△OEF的面积不小于2
2
，求直线l的斜率的取值范围．
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分．）
A．设函数f（x）=|2x+1|-|x-4|．则不等式f（x）＞2的解集为
{x|x＜-7或x＞
5
3
}
{x|x＜-7或x＞
5
3
}
；
B．（坐标系与参数方程选做题）曲线C：
x=-2+2cosα
y=2sinα
（α为参数），若以点O（0，0）为极点，x正半轴为极轴建立极坐标系，则该曲线的极坐标方程是
ρ=-4cosθ
ρ=-4cosθ
．

C．（几何证明选讲选做题） 如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，弧AE=弧AC，DE交AB于F，且AB=2BP=4，则PF=
3
3
．
A．如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC，DE交AB于点F．求证：△PDF∽△POC．
B．已知矩阵A=
.
1-2
3-7
.
．
（1）求逆矩阵A-1；
（2）若矩阵X满足AX=
3
1
，试求矩阵X．
C．坐标系与参数方程
已知极坐标系的极点O与直角坐标系的原点重合，极轴与x轴的正半轴重合，曲线C1：ρcos（θ+
π
4
）=2
2
与曲线C2：
x=4t2
y=4t
，（t∈R）交于A、B两点．求证：OA⊥OB．
D．已知x，y，z均为正数，求证：
x
yz
+
y
zx
+
z
xy
≥
1
x
+
1
y
+
1
z
．
曲线C上任一点到点E（-4，0），F（4，0）的距离的和为12，C与x轴的负半轴、正半轴依次交于A，B两点，点P在曲线C上且位于x轴上方，满足
PA
•
PF
=0．
（1）求曲线C的方程；
（2）求点P的坐标；
（3）以曲线C的中心O为圆心，AB为直径作圆O，是否存在过点P的直线l使其被圆O所截的弦MN长为3
15
，若存在，求直线l的方程；若不存在，请说明理由．
（1）如图，AB是⊙O的直径，AC是弦，∠BAC的平分线AD交⊙O于D，DE⊥AC交AC延长线于点E，OE交AD于点F．
（Ⅰ）求证：DE是⊙O的切线；
（Ⅱ）若
AC
AB
=
3
5
，求
AF
DF
的值．
（2）在直角坐标系中，以原点为极点，x轴的正半轴为极轴建坐标系，已知曲线
C：ρsin2θ=2acosθ（a＞0），已知过点P（-2，-4）的直线L的参数方程为：
x=-2+
2
2
t
y=-4+
2
2
t
，直线L与曲线C分别交于M，N．
（Ⅰ）写出曲线C和直线L的普通方程；  
（Ⅱ）若|PM|，|MN|，|PN|成等比数列，求a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网