Question

【题目】已知直线 （ 为参数）， ．
（1）当 时，求 与 的交点坐标；
（2）以坐标原点 为圆心的圆与 相切，切点为 ， 为 的中点，当 变化时，求 点的轨迹的参数方程，并指出它是什么曲线．

Answer 1

【答案】
（1）解：当 时， 的普通方程为 ， 的普通方程为

联立方程组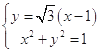

解得 与 的交点为（1,0），

（2）解： 的普通方程为

A点坐标为 ．∴当 变化时，P点轨迹的参数方程为

（ 为参数）P点轨迹的普通方程为

故P点轨迹是圆心为 ，半径为 的圆．

【解析】本题主要考查了直线的参数方程，解决问题的关键是掌握参数方程与普通方程相互转化，极坐标方程与直角坐标系方程相互转化
【考点精析】本题主要考查了直线的参数方程和圆的参数方程的相关知识点，需要掌握经过点，倾斜角为的直线的参数方程可表示为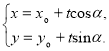（为参数）；圆的参数方程可表示为才能正确解答此题．